Задача синтеза и анализа дискретного фильтра, страница 5

Особенность выражения (3.2) по сравнению с (3.1) заключается в отличии от единицы свободного члена знаменателя, вследствие чего коэффициент b₀ появляется и в числителе, обеспечивая необходимую нормировку функции , а именно, . Следует подчеркнуть, что подобная нормировка должна быть соблюдена лишь при нечетном n (см. рис. 3.1, б). В противном случае необходимо, чтобы и при четном n соотношение (3.2) должно быть переписано в виде

                               ,

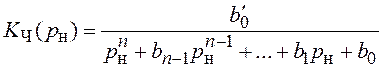где .

В табл. 3.2 приведены значения полюсов функции передачи [8] некоторых фильтров Чебышева при различных значениях неравномерности АЧХ b.

Таблица 3.2

После того как установлен вид функции передачи аналогового фильтра-прототипа , подстановкой (2.6) находится системная функция соответствующего дискретного фильтра:

                                            .

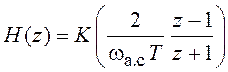При выполнении алгебраических преобразований полезно иметь в виду следующее:

·  знаменатель исходного выражения для , описываемого формулой (3.1), удобно записывать в форме, аналогичной представленной в табл. 3.2;

·  окончательное выражение для системной функции следует записывать с отрицательными степенями аргумента z, а его знаменатель представить в виде произведения сомножителей не выше второй степени.

В качестве примера приведем выражение для системной функции дискретного фильтра четвертого порядка в требуемой форме:

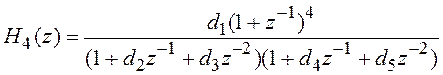                          ,                (3.8)

где  и  — вещественные коэффициенты.

Получив выражение для H(z) в форме (3.3), необходимо установить, соответствует ли оно устойчивому дискретному фильтру. При этом следует руководствоваться правилом: если все n полюсов системной функции H(z) лежат внутри окружности единичного радиуса на плоскости комплексной переменной z, то рассматриваемый дискретный фильтр устойчив.

Далее, естественно получить разностное уравнение, описывающее синтезируемый дискретный фильтр. Это можно сделать, если учесть, что соотношение (2.4) для системной функции H(z) = Y(z)/X(z) дискретного фильтра легко выводится из разностного уравнения (2.2) в результате применения к обеим его частям z‑преобразования. При этом используется свойство линейности z‑преобразования, а также тот факт, что запаздывание дискретного сигнала на один элемент соответствует умножению его z‑преобразования на z^–1. В конечном итоге, с целью перехода к разностному уравнению функция H(z) приводится к следующему виду:

                               ,

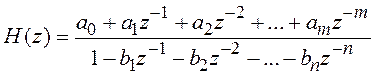где все коэффициенты являются вещественными и набор их в знаменателе, несмотря на общность обозначений, не совпадает с коэффициентами  (k = 1, 2, …, n – 1) в выражении (3.2). Запись системной функции в таком виде дает возможность осуществить проверку правильности преобразований при переходе от  к H(z), что весьма полезно как средство промежуточного контроля. В самом деле, поскольку H(1) = K(0), то для фильтров Баттерворта произвольного и Чебышева нечетного порядков справедливо равенство

                               ,

так как в этом случае K(0) = 1.

Для фильтра Чебышева четного порядка подобное выражение выглядит иначе, а именно:

              ,

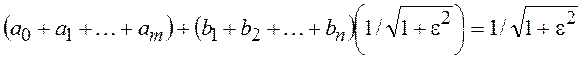где  при четных n.

Проверку необходимо провести, прежде чем приступать к реализации структурных схем ДФ.

Следуя методике построения структурных схем ДФ, изложенной в [1]–[7], требуется реализовать полученную системную функцию в прямой, канонической, параллельной и последовательной формах.