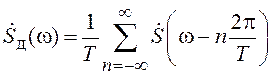 ,
,
указывающее, что спектр
дискретизированного сигнала ![]() является периодическим
повторением спектра непрерывного сигнала (сравните с соотношением (2.5) для АЧХ дискретного фильтра). Заметим, что сигнал
является периодическим
повторением спектра непрерывного сигнала (сравните с соотношением (2.5) для АЧХ дискретного фильтра). Заметим, что сигнал ![]() — это не то же самое, что последовательность отсчетов
x(kT)
непрерывного сигнала, а функция:
— это не то же самое, что последовательность отсчетов
x(kT)
непрерывного сигнала, а функция:
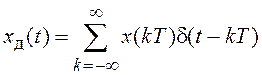 ,
,
где d(t) — дельта-функция Дирака.
Максимально плоская АЧХ аналогового ФНЧ описывается выражением
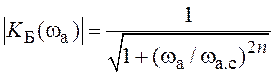 , (3.1)
, (3.1)
где ![]() — частота среза аналогового фильтра, на которой АЧХ
падает до уровня 0,707 от своего максимального значения; n = 1, 2, 3, … —
порядок фильтра; индекс «а» при обозначении текущего значения частоты подчеркивает,
что речь идет об аналоговом фильтре. Возможный вид
— частота среза аналогового фильтра, на которой АЧХ
падает до уровня 0,707 от своего максимального значения; n = 1, 2, 3, … —
порядок фильтра; индекс «а» при обозначении текущего значения частоты подчеркивает,
что речь идет об аналоговом фильтре. Возможный вид ![]() представлен
на рис. 3.1, а.
представлен
на рис. 3.1, а.
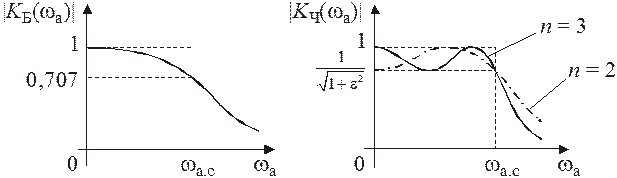
а б
Рис. 3.1
Для полного описания данной АЧХ
необходимо установить две величины: частоту среза ![]() и
порядок фильтра n. Первая из них
рассчитывается в соответствии с соотношением (2.7),
в которое должны войти определенные в 3.2 интервал
дискретизации Т и значение
и
порядок фильтра n. Первая из них
рассчитывается в соответствии с соотношением (2.7),
в которое должны войти определенные в 3.2 интервал
дискретизации Т и значение ![]() . Порядок аналогового фильтра определяется
из условия обеспечения необходимого затухания a его АЧХ на удвоенной частоте среза
. Порядок аналогового фильтра определяется
из условия обеспечения необходимого затухания a его АЧХ на удвоенной частоте среза ![]() . Это условие записывается
таким образом:
. Это условие записывается
таким образом:
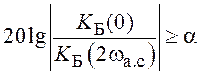
и позволяет определить минимально возможный порядок фильтра n.
Выражение для равноволновой в полосе пропускания АЧХ ФНЧ Чебышева имеет следующий вид:
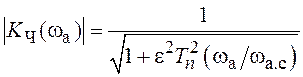 , (3.2)
, (3.2)
где e — параметр, характеризующий неравномерность АЧХ в
полосе пропускания; ![]() —
полином Чебышева первого рода порядка n.
Полиномы низших степеней таковы:
—
полином Чебышева первого рода порядка n.
Полиномы низших степеней таковы:
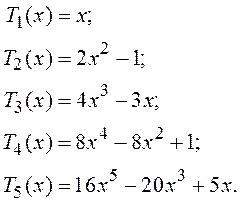 (3.3)
(3.3)
АЧХ ![]() приведена
на рис. 3.1, б.
Соотношение (3.1) содержит три параметра, подлежащих определению, а именно:
приведена
на рис. 3.1, б.
Соотношение (3.1) содержит три параметра, подлежащих определению, а именно: ![]() , e
и n. Частота среза аналогового фильтра
, e
и n. Частота среза аналогового фильтра ![]() находится так же, как и в 3.3.1.
Значение e вычисляется по заданной
неравномерности b АЧХ в полосе
пропускания фильтра. При этом следует исходить из выражения
находится так же, как и в 3.3.1.
Значение e вычисляется по заданной
неравномерности b АЧХ в полосе
пропускания фильтра. При этом следует исходить из выражения
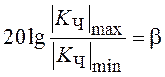 , (3.4)
, (3.4)
где ![]() —
наибольшее и наименьшее значения АЧХ фильтра Чебышева в полосе пропускания,
причем необходимо заметить, что значения эти от порядка фильтра не зависят.
Последний определяется, как и в 3.3.1, приведенным в задании значением
затухания АЧХ a, но более сложным
образом.
—
наибольшее и наименьшее значения АЧХ фильтра Чебышева в полосе пропускания,
причем необходимо заметить, что значения эти от порядка фильтра не зависят.
Последний определяется, как и в 3.3.1, приведенным в задании значением
затухания АЧХ a, но более сложным
образом.
Следует решить неравенство вида
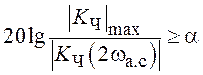 , (3.5)
, (3.5)
где ![]() имеет тот же смысл, что и в
соотношении (3.3), а
имеет тот же смысл, что и в
соотношении (3.3), а ![]() определяется уже упомянутым
параметром e и значением полинома
Чебышева порядка n при x = 2, т. е.
определяется уже упомянутым
параметром e и значением полинома
Чебышева порядка n при x = 2, т. е. ![]() .
Следовательно, установив из неравенства (3.4) требование к значению
.
Следовательно, установив из неравенства (3.4) требование к значению ![]() , необходимо, пользуясь формулами (3.2), подобрать наименьшее подходящее значение n,
которое и будет порядком фильтра.
, необходимо, пользуясь формулами (3.2), подобрать наименьшее подходящее значение n,
которое и будет порядком фильтра.
При синтезе дискретного фильтра методом билинейного z‑преобразования его системную функцию H(z) определяют исходя из коэффициента передачи аналогового фильтра-прототипа K(p), записанного в операторной форме. При этом используется подстановка (2.6). Функция передачи фильтра Баттерворта нижних частот порядка n записывается как
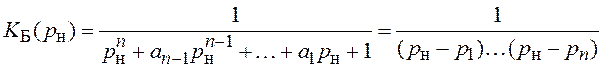 , (3.6)
, (3.6)
где ![]() ; a1,
a2, …, an – 1 — вещественные
коэффициенты; p1, p2, …, pn — полюсы функции
; a1,
a2, …, an – 1 — вещественные
коэффициенты; p1, p2, …, pn — полюсы функции ![]() .
.
Выражения знаменателя функции передачи для некоторых фильтров Баттерворта [8] приведены в табл. 3.1.
Таблица 3.1
|
n |
Знаменатель функции |
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
Для фильтра Чебышева нечетного порядка
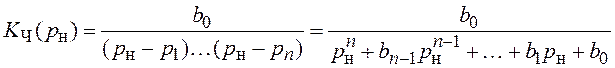 . (3.7)
. (3.7)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.