Задача синтеза и анализа дискретного фильтра, страница 6

Для построения прямой схемы реализации дискретного фильтра алгоритм дискретной фильтрации должен быть представлен в следующем виде:

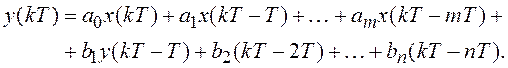
Приведенная форма записи алгоритма дискретной фильтрации позволяет изобразить структурную схему ДФ непосредственно. Ее называют прямой или основной формой реализации ДФ. Эта схема представлена на рис. 3.2.

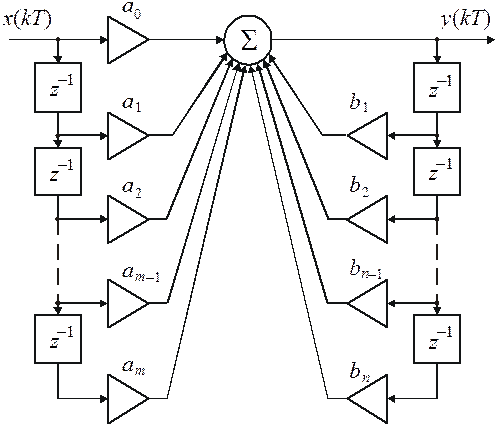
Рис. 3.2

Число элементов задержки удается минимизировать в так называемой канонической схеме дискретного фильтра. Для ее реализации необходимо:

а) выражение (2.4) для системной функции Н(z) представить в форме

H(z) = H₁(z) H₂(z),

где

                            ,

                               ;

б) независимо синтезировать структурные схемы для системных функций H₁(z) и H₂(z) в прямой форме и соединить их каскадно. При этом используют разностные уравнения, которые для указанных функций будут иметь вид:

                     ,

                 .

Соответствующие структурные схемы изображены на рис. 3.3. H₂(z) соответствует нерекурсивному дискретному фильтру, отсчетные значения сигнала на выходе которого формируются только на основе значений входного сигнала. Если же используются и предыдущие выходные отсчеты, как в схеме для H₁(z), то фильтр называется рекурсивным;

в) сократить лишние элементы задержки, возникающие при каскадном соединении схем, представленных на рис. 3.3.

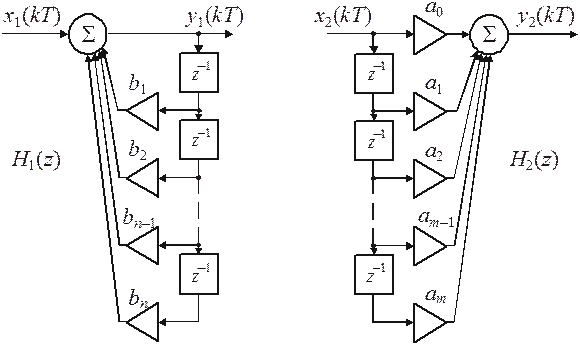
                                              а                                                                б

Рис. 3.3

Каноническая схема ДФ при этом должна быть представлена в виде, изображенном на рис. 3.4 (для определенности принято n > m). В современной литературе дискретные фильтры принято делить на две группы: фильтры с конечными (КИХ) и бесконечными (БИХ) во времени импульсными характеристиками. КИХ-фильтры можно эффективно строить как по рекурсивной, так и по нерекурсивной схемам, а БИХ-фильтры синтезируются лишь на основе рекурсивного алгоритма.

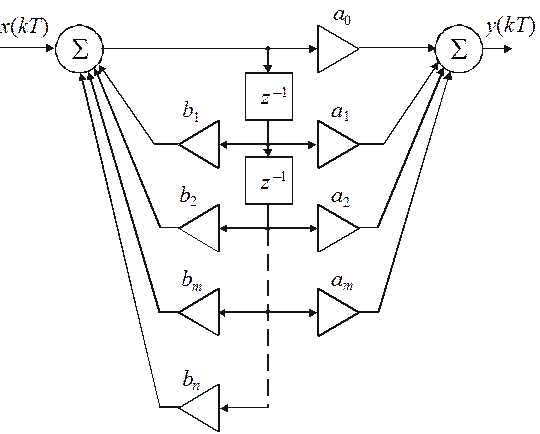
Рис. 3.4

Реализация последовательной и параллельной схем ДФ производится при представлении исходной системной функции в виде соответственно произведения или суммы [1]–[4] нескольких парциальных системных функций:

                                     ;

,

каждая из которых соответствует дискретному фильтру порядка не выше второго (порядок фильтра равен числу полюсов его системной функции).

3.5. Анализ АЧХ дискретного фильтра

Известная системная функция дискретного фильтра позволяет, как видно из выражения (2.5), определить его АЧХ:

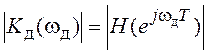                                             .                                    (3.5)

Обозначение частоты с индексом введено здесь, чтобы избежать путаницы при трансформации частотной оси в методе билинейного z‑преобразования.

Пользуясь приведенным соотношением, следует рассчитать АЧХ дискретного фильтра, причем в силу периодичности рассматриваемых функций расчет нужно проводить лишь для . Кроме того, при построении АЧХ чебышевского типа необходимо выбрать достаточно малый шаг по частоте, чтобы не пропустить характерные точки, соответствующие максимумам и минимумам АЧХ в полосе пропускания дискретного фильтра.

Как следует из [1]–[3], по сравнению с АЧХ аналогового фильтра-прототипа АЧХ дискретного фильтра искажается только вдоль частотной оси согласно формуле (2.7). Поэтому АЧХ аналогового фильтра-прототипа  и АЧХ дискретного фильтра , синтезированного на основе данного прототипа методом билинейного z‑преобразования, связаны следующим образом:

                                           .

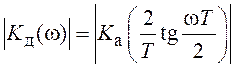С целью оценки этих искажений необходимо рассчитать АЧХ аналогового фильтра Баттерворта  или Чебышева , имеющего ту же частоту среза , что и синтезированный дискретный фильтр. Эти характеристики описываются следующим образом:

       ,       .

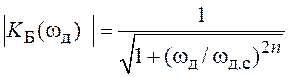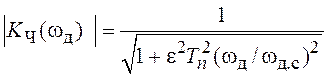Графики одной из данных зависимостей и функции (3.1) следует для сопоставления построить совместно, ограничившись, как уже указывалось, интервалом изменения  от 0 до p/T. При правильном расчете системной функции дискретного фильтра коэффициент передачи на частоте среза  должен оказаться одинаковым для обоих графиков.

3.6. Расчет импульсной характеристики