Задача синтеза и анализа дискретного фильтра, страница 8

2. Знаменатель второго слагаемого (3.8) необходимо разложить на множители вида , где p_i — полюсы системной функции. В исходном выражении (3.7) уже был выделен вещественный полюс, равный 0,5. Два оставшихся полюса являются комплексно-сопряженными и находятся путем решения квадратного уравнения :

                                    .

В результате (3.8) принимает вид

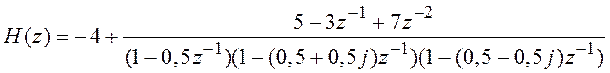            .   (3.9)

3. Второе слагаемое (3.9) раскладывается на сумму простейших дробей

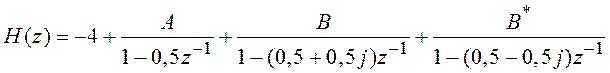            . (3.10)

Сопоставляя выражения (3.9) и (3.10), определяют значения коэффициентов: A = 27; B = –11 – 2j; B* = –11 + 2j. Таким образом, окончательное представление системной функции в виде суммы простейших дробей имеет вид

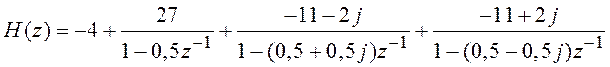            . (3.11)

4. Первому слагаемому в (3.11) соответствует слагаемое импульсной характеристики вида

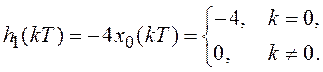
Здесь x₀(kT) — единичный дискретный сигнал.

Остальные три слагаемых представляют собой суммы бесконечных геометрических прогрессий:

                                        ,

                     ,

                     .

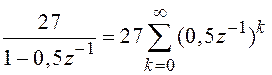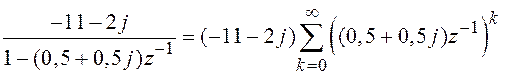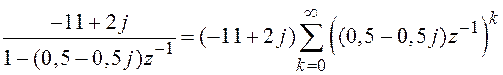Эти слагаемые дают в импульсную характеристику вклад в виде трех геометрических прогрессий. Для удобства записи комплексные коэффициенты целесообразно представить в экспоненциальной форме:

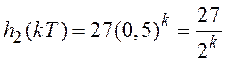,     k ³ 0,

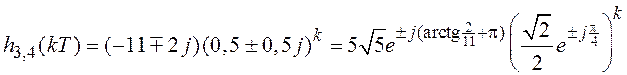,     k ³ 0.

5. Полная импульсная характеристика рассматриваемого дискретного фильтра представляет собой сумму полученных слагаемых:

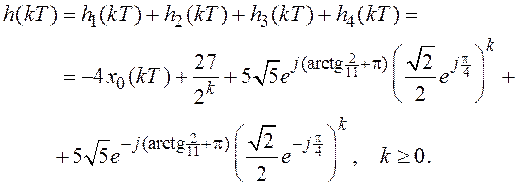                             (3.12)

6. Полученное выражение (3.12) является вещественным, но содержит два комплексно-сопряженных слагаемых. Поэтому в качестве последнего шага от этих слагаемых нужно избавиться, суммируя их по формуле Эйлера ():

3.7. Определение сигналов на выходе дискретного фильтра

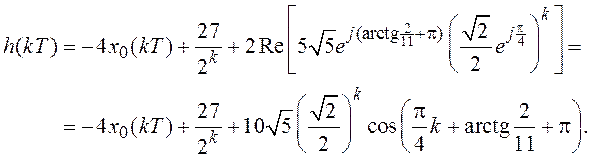
Курсовая работа завершается решением задачи анализа синтезированного фильтра во временной области. Постановка ее проста и состоит в следующем. Имеется ДФ с импульсной характеристикой h(kT), вычисленной в 3.6. На его вход поступает последовательность отсчетов, рассчитанная в 3.2 в результате дискретизации непрерывного входного сигнала u(t). Данную задачу целесообразно решать методом дискретной свертки:

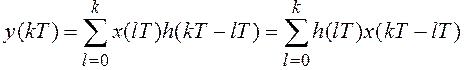                        .               (3.1)

Процедура вычисления дискретной свертки является достаточно трудоемкой. Ее можно осуществить двумя путями, а именно: следуя непосредственно выражению (3.1) или применяя косвенный, основанный на использовании дискретного преобразования Фурье [1]–[7], метод вычисления. В любом случае расчеты целесообразно выполнять с помощью компьютера.

Используя программу FILTER, необходимо не только определить сигнал на выходе ДФ при воздействии на его вход последовательности отсчетов x(kT), но исследовать также прохождение через синтезированный фильтр двух-трех сигналов произвольного вида. Сигналы задаются преподавателем. По умолчанию, целесообразно рассмотреть прохождение двух аналоговых сигналов стандартной формы, а именно: треугольного видеоимпульса и видеоимпульса в виде периода меандра. Значение длительности импульсов удобно взять постоянным и равным длительности T₂ исходного сигнала, а максимальное значение — равным такому же параметру заданного сигнала u(t). Простая структура сигналов позволяет сохранить прежним интервал дискретизации T; следовательно, не изменится число отсчетов в последовательности, соответствующей результату дискретизации аналогового сигнала.

Программа FILTER также дает возможность углубить содержание курсовой работы за счет введения в рассмотрение случайного дискретного сигнала , представляющего собой последовательность отсчетов, являющихся статистически независимыми значениями непрерывной нормально распределенной случайной величины  с заданными значениями математического ожидания  и дисперсии , где  — среднеквадратичное значение . Анализ прохождения случайного сигнала через дискретный фильтр сводится к сопоставлению оценок математических ожиданий, дисперсий и сравнению корреляционных функций (КФ) входного  и выходного  дискретных сигналов. С использованием программы FILTER необходимо выполнить следующее.

1. Сформировать последовательность из 20…25 отсчетов входного случайного сигнала  с математическим ожиданием  и дисперсией .