Реакция системы на входное воздействие типа v = const представляет собой экспоненту, скорость затухания которой определяется параметром T, а установившееся значение (статика) для выходной переменной соответствует выражению
|
|
(5.39) |
Процесс считают закончившимся, когда выходная переменная достигает установившегося значения с точностью не менее 5% .
|
Риc.5.20. Переходный процесс
в системе |
Система (5.38) имеет только
один корень характеристического уравнения, поэтому
|
![]()
![]() В начало
В начало
5.6.2. Система 2-го порядка
Стандартное описание такой системы следующее:
|
|
(5.41) |
Переходные процессы в ней зависят от трех параметров: коэффициента передачи k, который определяет установившееся значение для выходной переменной в соответствии с выражением (5.24); постоянной времени T и коэффициента демпфирования d.
В литературе приводятся нормированные переходные характеристики в зависимости от d. Качественный вид их представлен на рис.5.21.
|
Риc.5.21. Переходные процессы в системе 2-го порядка |
В системе 2-го порядка
время переходного процесса зависит не только от постоянной времени T, но и от
коэффициента демпфирования d, поэтому для его приближенной оценки можно
пользоваться соотношением (5.40), если d изменяется в диапазоне |
Корни характеристического уравнения системы следующие:
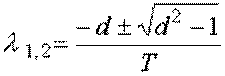 ,
,
что позволяет определить колебательность (при d < 1) в виде
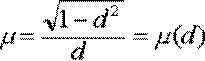 .
.
Таким образом, коэффициент демпфирования d определяет колебательность системы, а следовательно, и ее перерегулирование.
5.6.3. Система 3-го порядка
Стандартная передаточная функция системы имеет вид:
|
|
(5.42) |
Таким образом, переходные процессы определяют уже четыре параметра: k, T, A, B.
Установившееся значение для выходной переменной соответствует выражению (5.39), то есть зависит только от коэффициента усиления k, инерционность процессов зависит от T, а колебательные свойства системы определяются параметрами A и B.
Для исследования этой зависимости используется диаграмма Вышнеградского, полученная им в 1876 году на основе характеристического уравнения
|
|
(5.43) |
Поскольку при оценке колебательности быстродействие нас не интересует, перейдем к нормированному характеристическому уравнению заменой в (5.43) Tp оператором q:
|
|
(5.44) |
где A и B -параметры Вышнеградского.
Введем в рассмотрение область значений параметров А и В и нанесем границу устойчивости, соответствующую условию:
|
A B = 1 . |
(5.45) |
Разобьем ее на подобласти с различным распределением корней характеристического уравнения (5.44), а значит и видом переходных процессов (рис.5.22).
Чтобы оценить вид переходного процесса, необходимо отметить точку с соответствующими значениями параметров A и B на диаграмме Вышнеградского.
Рис.5.22. Диаграмма Вышнеградского
|
Рис.5.23. Апериодический процесс |
Если она попала в область, где все корни вещественные (область 3), процесс будет иметь апериодический характер (рис.5.23). |
|
Рис.5.24. Колебательный процесс |
Если точка соответствует области 1, где ближайшей к мнимой оси будет пара комплексно - сопряженных корней, то это - область колебательных процессов (рис.5.24). |
|
Рис.5.25. Монотонный процесс |
В случае, когда вещественный корень располагается ближе к мнимой оси, чем пара комплексно - сопряженных (область 2), колебательная составляющая затухает быстрее, и процессы будут носить монотонный характер. |
Литература к пятой главе: [3], [6], [14], [16]-[18].
Задание текущего контроля №2
Итоговое задание
![]()
![]() В начало
В начало
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.