Анализ переходных процессов. Корневой метод анализа. Анализ систем низкого порядка, страница 4

В (5.26) подынтегральная функция четная, поэтому можно перейти к интегрированию по положительным частотам и удвоить результат, что дает

.

(5.27)

Здесь время t является параметром, так как интегрирование осуществляется по . В то же время известно, что импульсная функция при t < 0 отсутствует, то есть g(-t) = 0. Это свойство используем для упрощения выражения (5.27), где в результате замены t на -t получим:

.

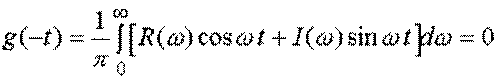Отсюда следует что

.

(5.28)

После подстановки (5.28) в (5.27) получим два соотношения для импульсной функции:

.

(5.29)

.

(5.30)

В расчетной практике чаще используется вещественная частотная характеристика и соотношение (5.29).

Обычно для анализа бывает необходима переходная характеристика, поэтому установим ее связь с вещественной частотной характеристикой.

В начало

5.4.3. Взаимосвязь между частотной и переходной характеристиками

Поскольку переходная функция связана с импульсной функцией соотношением

,

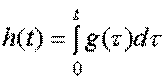то после подстановки в него (5.27) получим

.

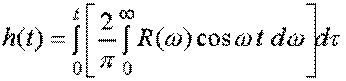Здесь произведение R ()cos t - функция двух переменных, поэтому изменим порядок интегрирования и запишем

.

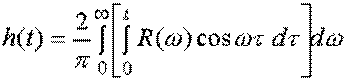В результате получим следующее соотношение, связывающее переходную и вещественную частотную характеристики:

.

(5.31)

Типичный вид вещественной частотной характеристики, которая может быть получена экспериментально, представлен на рис.5.11.

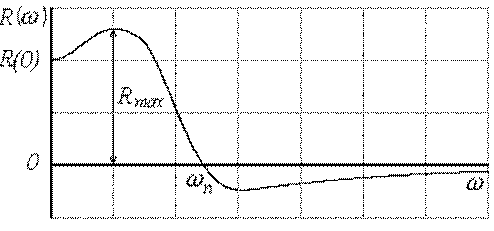
Риc.5.11. Вещественная частотная характеристика системы

В теории управления было разработано несколько способов вычисления переходной характеристики по виду R( ), например, методы трапеций и треугольников.

В настоящее время необходимость в них отпала, так как с помощью средств вычислительной техники можно с достаточной степенью точности построить характеристики h(t).

Однако, выражение (5.31) используется для оценки вида переходного процесса без построения всей кривой h(t).

В начало

5.4.4. Оценки качества переходного процесса
по вещественной частотной характеристике

Такие оценки оказываются особенно удобными в случае, когда для исследования системы применяются частотные методы, а переходный процесс вызван скачкообразным входным воздействием.

На основании анализа соотношения (5.31) были получены следующие оценки качества переходного процесса.

Оценка 1. Начальное значение переходной характеристики соответствует конечному значению ВЧХ.

, как правило, h (0)=0.

Оценка 2. Конечное значение переходной характеристики равно начальному значению ВЧХ.

, как правило, h()=k .

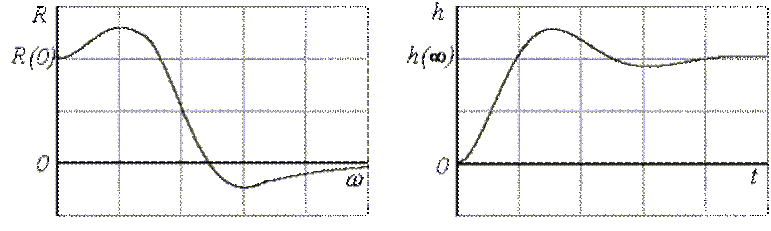
Риc.5.12. Иллюстрация 1-ой и 2-ой оценок

Оценка 3. Если для частотных характеристик двух систем справедливо выражение

или ,

то аналогичное соотношение будет связывать и переходные характеристики:

(t) = m (t) или (t) = (t) .

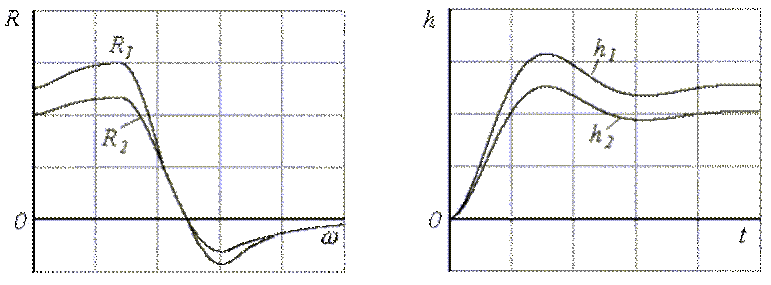
Рис.5.13. Иллюстрация 3-ей оценки

Оценка 4. В случае, когда частотные характеристики двух систем связаны соотношением

,

для переходных характеристик справедливо равенство

.

Рис.5.14. Иллюстрация 4-ой оценки

Оценка 5. Если R() является положительной невозрастающей функцией, то перерегулирование в системе не будет превышать 18%.

Оценка 6. Переходная характеристика имеет монотонный характер, если представляет собой отрицательную, убывающую по модулю непрерывную функцию.

Оценка 7. В случае, когда R () есть локально возрастающая функция, перерегулирование можно оценить по формуле:

Рис.5.15. Иллюстрация 7-ой оценки

• 

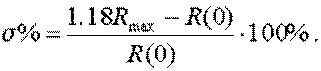
Оценка 8. Если на какой-то частоте R() терпит разрыв, то переходная характеристика будет иметь незатухающие колебания этой частоты.

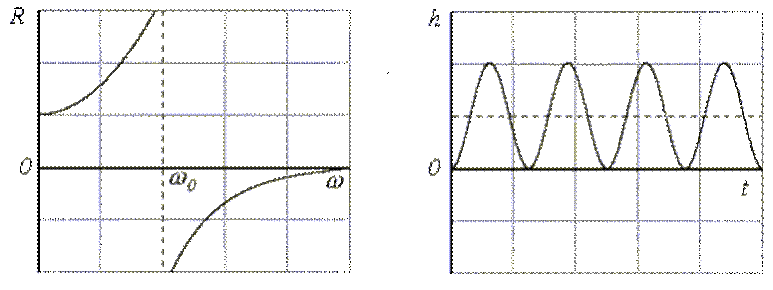
Рис.5.16. Иллюстрация 8-ой оценки

Оценка 9. Для монотонных процессов время переходного процесса можно приближенно оценить по формуле:

, .

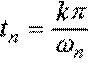Если частотная характеристика R ( ) всегда положительна, то в качестве выбирается частота, на которой .