Другие предметы \ Теория автоматического управления

Анализ переходных процессов. Корневой метод анализа. Анализ систем низкого порядка, страница 2

В начало

5.2.3. Перерегулирование

Эта количественная оценка характеризует колебательные свойства системы, обозначается буквой и определяется в процентах относительно установившегося значения по выражению

.

(5.9)

Риc.5.4. Иллюстрация оценки перерегулирования

Чем больше перерегулирование , тем более система склонна к колебаниям.

В начало

5.2.4. Интегральные оценки

Интегральные оценки представляют собой обобщенные показатели качества переходного процесса. Обычно для их определения используют динамическую ошибку.

<>

Риc.5.5. Динамическая ошибка системы

В качестве интегральной оценки можно использовать следующие величины:

1)

,

(5.10)

которая дает надежные результаты только в случае монотонного переходного процесса.

2)

(5.11)

характеризует площадь под кривой на рис.5.5.

3)

.

(5.12)

Наиболее удобной из приведенных является интегральная оценка , которая сравнительно просто вычисляется и применяется как для монотонного, так и для колебательного процесса. Она характеризует также затраты энергии на совершение переходного процесса.

Риc.5.6. Идеальный переходный процесс

Идеальный переходный процесс (без лишних потерь энергии) представлен на рис.5.6.

В общем виде интегральная оценка качества переходного процесса записывается следующим образом:

.

(5.13)

Применение конкретной интегральной оценки зависит от вида переходного процесса и требований, предъявляемых к системе.

В начало

5.3. Анализ статических режимов

Статическим называют такой установившийся режим работы системы, при котором переменные системы, а также входные воздействия и внешние возмущения с течением времени не изменяются. Величина статической ошибки , характеризующей данный режим, позволяет разделить все системы на несколько типов.

5.3.1. Статические системы

Статической будем называть такую систему управления, функционирование которой возможно только при наличии статической ошибки .

Рассмотрим работу системы со следующей структурной схемой:

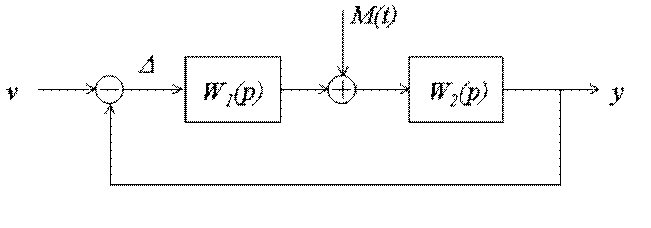
Рис.5.7. Структурная схема статической системы

Здесь - передаточные функции, не содержащие в своем составе интегрирующих звеньев, поэтому в статике они принимают вид: . Обычно первый блок представляет собой регулятор а второй - объект управления

Запишем выражение для ошибки в операторной форме,

или после преобразований

(5.14)

Полная ошибка регулирования складывается из двух составляющих: ошибки по входному воздействию и по возмущению. Полагая в выражении (5.14) p= 0, получим статическую ошибку

(5.15)

Здесь-общий коэффициент усиления, характеризующий глубину обратной связи.

Особое значение статическая ошибка имеет в системах стабилизации, когда требуется обеспечить выполнение свойства (5.3), то есть lim y(t) = v при . Для этих систем входное воздействие постоянно (v =const), а возмущение меняется произвольным образом ( M = var). Составляющая ошибки, порожденная входным воздействием, может быть уменьшена путем масштабирования, поэтому важной является зависимость ошибки от возмущения.

Рис.5.8. Зависимость статической ошибки от возмущения

Согласно выражению (5.15), статическая ошибка по входному воздействию определяется величиной k, а ошибка по возмущению зависит только от .

Следовательно, для уменьшения полной ошибки необходимо увеличивать коэффициент усиления, прежде всего . Однако, его чрезмерное увеличение может привести к неустойчивости системы.

В начало

5.3.2. Астатические системы

Астатическими называются системы, в которых отсутствует составляющая статической ошибки, порожденная входным воздействием. Астатизм обычно достигается введением в регулятор интегрирующего звена (рис.5.9).

Скачать файл