Анализ переходных процессов. Корневой метод анализа. Анализ систем низкого порядка, страница 5

<> Рис.5.17. Иллюстрация 9-ой оценки

Рис.5.18. Определение частоты

Таким образом, с помощью приведенных оценок можно приближенно (без вычислений) оценить качество переходного процесса по виду вещественной частотной характеристики.

Подробно частотные оценки переходного процесса описаны в работах В.В. Солодовникова.

·  В начало

5.4.5. О начальном участке переходной характеристики

Используя частотный метод, можно оценить не только начальное значение переходного процесса, но и его вид на начальном участке.

Рассмотрим систему с передаточной функцией общего вида:

.

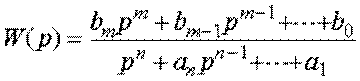Заменив p на j , перейдем к ее частотной характеристике

.

(5.32)

Известно, что начальное значение переходного процесса определяет конец частотной характеристики, поэтому в (5.32) устремим . При этом доминирующими слагаемыми в числителе и знаменателе будут в старшей степени, и (5.32) вырождается в

.

(5.33)

Частотную характеристику (5.33) имеет интегратор (n-m) порядка, следовательно, и начальный участок переходного процесса соответствует интегратору (n-m) порядка.

В случае, когда передаточная функция системы n-го порядка содержит в числителе просто коэффициент, начальный участок переходного процесса соответствует степенной функции n-го порядка.

В начало

5.5.Корневой метод анализа

5.5.1. Введение

Данный метод анализа, в отличие от частотного, позволяет исследовать реакцию системы на начальные условия (первое слагаемое решения (5.2) и может применяться как для одноканальных, так и многоканальных систем.

Для одноканальных систем вида

,

(5.34)

общая реакция на входной сигнал при ненулевых начальных условиях описывается соотношением

,

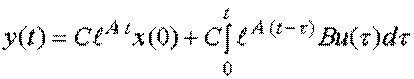которое является частным случаем (5.2).

Нас интересует первая составляющая правой части уравнения, представляющая собой линейную комбинацию мод (2.39):

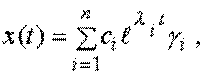
где - корни характеристического уравнения.

Каждая мода эквивалентна решению системы первого или второго (если корни комплексно - сопряженные) порядка, причем скорость затухания соответствующей экспоненты зависит от численного значения . Поэтому на основе корней характеристического уравнения можно оценить граничные составляющие переходного процесса: самую быструю, самую колебательную моду и т.п.

В начало

5.5.2. Корневые оценки переходного процесса

Будем рассматривать характеристическое уравнение системы

с корнями , которые изобразим на комплексной плоскости.

Риc.5.19. Корневой портрет системы

Наиболее удаленные от мнимой оси корни (имеющие max) определяют моды, затухающие быстрее всего. Корни характеристического уравнения, расположенные ближе всего к мнимой оси (с min ), дают наиболее медленно затухающие моды, которые и определяют длительность переходного процесса.

Поэтому корневой оценкой быстродействия служит расстояние до мнимой оси ближайшего к ней корня, то есть

, .

(5.35)

В случае, когда статическая ошибка 5%, можно приближенно оценивать время переходного процесса (время попадания в 5% зону) по соотношению:

.

(5.36)

Колебания в системе будет наблюдаться только в том случае, когда характеристическое уравнение содержит комплексно - сопряженные корни

. Склонность системы к колебаниям характеризует величина

,

(5.37)

которая называется колебательностью. Чем больше , тем более колебательными будут переходные процессы системы и наоборот. При колебания отсутствуют, процессы будут носить апериодический характер. Обычно допустимая колебательность системы .

В начало

5.6.Анализ систем низкого порядка

5.6.1. Система 1-го порядка

Качество процессов в системе 1-го порядка, которая описывается с помощью стандартной передаточной функции,

,

(5.38)

зависит от коэффициента передачи k и постоянной времени T.