Анализ переходных процессов. Корневой метод анализа. Анализ систем низкого порядка, страница 3

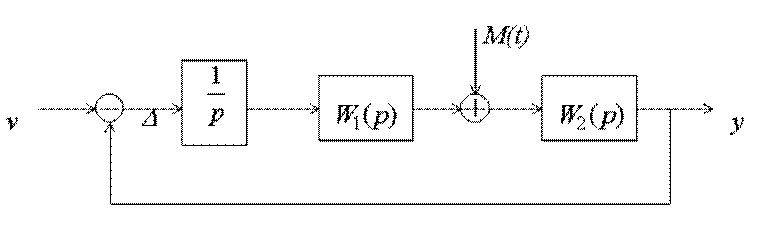
Рис.5.9. Структурная схема астатической системы

Полагая, что - передаточные функции, не содержащие в своем составе интегрирующих звеньев, определим ошибку в системе

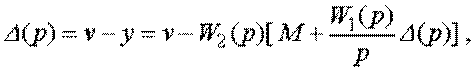
которая после преобразований принимает вид

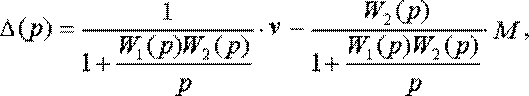
или окончательно

(5.16)

Как следует из (5.16), в статике будет равна нулю не только ошибка по входному воздействию, но и ошибка по возмущению, то есть

.

(5.17)

Для астатических систем представляет интерес режим ‘‘линейной заводки’’, при котором входной сигнал v есть линейная функция времени

v(t) = v(0) ,

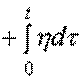или в операторной форме

v(p) ,

(5.18)

где const .

Подставим v(р) в выражение для ошибки (5.16)

,

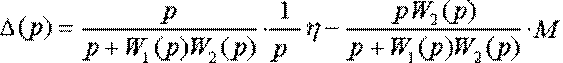откуда в установившемся режиме (при p =0) получим скоростную ошибку

.

(5.19)

Для уменьшения можно масштабировать входное воздействие или увеличивать общий коэффициент усиления системы k .

В начало

5.3.3. Следящие (позиционные) системы

Этим термином обозначают класс систем, в которых выходная переменная объекта должна отслеживать (повторять) изменения входной величины.

Структурным признаком таких систем является наличие интегратора на выходе.

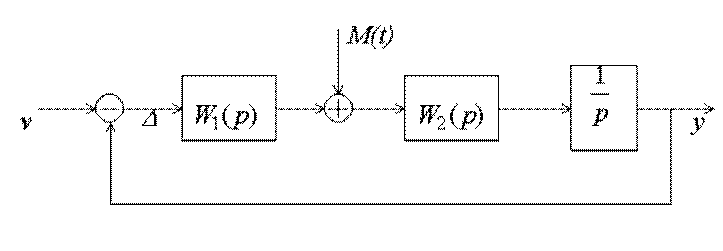
Рис.5.10. Структурная схема следящей системы

Выражение для ошибки в такой системе имеет вид:

.

(5.20)

Как видим, в статике (при р=0 ) первая составляющая статической ошибки обращается в ноль, но остается вторая составляющая, порожденная возмущением:

.

(5.21)

Таким образом, следящие системы также являются астатическими по входному воздействию, однако, они всегда имеют статическую ошибку по возмущению, зависящую от коэффициента .

Рассмотрим режим ‘‘линейной заводки’’, когда 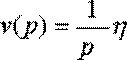. В этом случае установившаяся (скоростная) ошибка представляет собой сумму двух составляющих

.

(5.22)

Режим ‘‘линейной заводки’’ используется для оценки точности астатических систем, в первую очередь следящих, для которых он является характерным режимом работы.

5.4.Частотный метод анализа

5.4.1. Введение

В большинстве случаев аналитическое вычисление переходной характеристики системы является трудоемкой задачей, поэтому используют косвенные методы оценки качества процессов.

Известно, что между переходными и частотными характеристиками системы, которые легко вычисляются, а также могут быть получены экспериментальным путем, существует однозначное соответствие. Поэтому качество переходных процессов можно исследовать непосредственно по ее частотным характеристикам.

Отметим, что частотный метод анализа позволяет оценить реакцию системы на входное воздействие v(t) при нулевых начальных условиях (второе слагаемое решения (5.2)).

5.4.2. Взаимосвязь между частотной характеристикой и импульсной функцией

Будем рассматривать линейную систему с известной передаточной функцией

,

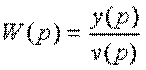от которой с помощью замены p на j перейдем к ее частотной характеристике W(j).

Соответствие между импульсной функцией и частотной характеристикой устанавливает обратное преобразование Фурье

.

(5.23)

Представим частотную характеристику W(j следующим образом:

,

(5.24)

а экспоненту на основе формулы Эйлера запишем в виде:

.

(5.25)

В результате подстановки (5.24) и (5.25) в выражение (5.23) получим

.

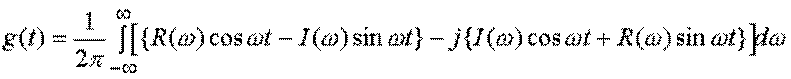Импульсная функция является вещественной, поэтому в последнем выражении мнимая часть должна быть равна нулю. Это нетрудно показать.

Здесь cos(t) есть четная функция частоты, а sin(t) - нечетная. Вещественная часть R() содержит четные степени частоты, и является четной функцией; мнимая часть, - нечетная. Следовательно, произведения R()sin(t ) и I()cos(t ) представляют собой нечетные функции, а интегрирование их суммы во всемдиапазоне частот дает

.

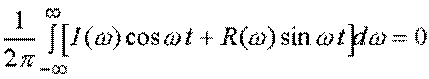Таким образом, выражение для импульсной функции принимает вид:

.

(5.26)