10.4. Расширенные модели экономического роста
Модели экономического роста, анализировавшиеся в 10.1, 10.2, отображают воспроизводство общественного продукта и национального дохода вне зависимости от других элементов общественного воспроизводства. В них не учитывается влияние трудовых ресурсов и уже созданных производственных фондов на динамику и структуру национального дохода; производственное накопление не связывается с необходимостью повышения производительности труда. Факторные же модели экономического роста, рассматривавшиеся в 10.3, исходят из экзогенной динамики производственных факторов, т.е. являются чрезмерно "открытыми". Объединение условий простых макроэкономических моделей позволяет преодолевать их односторонность.
Синтез производственной функции и балансов производственных ресурсов. Макроэкономические производственные функции логично дополнить балансами трудовых ресурсов и основных производственных фондов, характеризующими процессы формирования величин L(t) и K(t).
Предварительно уточним ряд понятий, использовавшихся ранее. В данном разделе величина у означает конечный продукт (национальный доход плюс возмещение выбытия основных производственных фондов), и — валовые производственные капитальные вложения (накопление и возмещение выбытия основных производственных фондов). Принимается, что возмещение выбытия составляет gK(t), где g— фиксируемый параметр. Таким образом,
u(t) = 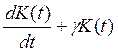 .(10.35)
.(10.35)
Динамика трудовых ресурсов достаточно хорошо описывается трендовыми
моделями. Для последующего анализа удобнее всего выбрать экспоненту.
Тогда в момент t величина трудовых ресурсов производственной сферы
составит L(0)elt, где L(0) - ресурсы в
момент t — 0; l— темп прироста трудовых ресурсов. Потребность
же в трудовых ресурсах в момент tсоставляет 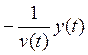 , где v (t) — функция производительности труда
(например, (10.32) или (10.33)).
, где v (t) — функция производительности труда
(например, (10.32) или (10.33)).
С учетом принятых допущений получаем баланс трудовых ресурсов производственной сферы:
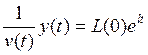 (10.36)
(10.36)
откуда определяется максимально возможный объем конечного продукта с точки зрения обеспеченности трудовыми ресурсами:
![]() (10.37)
(10.37)
Очевидно, что при неизменной производительности труда конечный продукт может расти темпом, не превышающим l. Если же экзогенный (или гарантированный) темп прироста производительности труда равен d, то
![]() (10.38)
(10.38)
Результаты 10.1 - 10.2 необходимо дополнить следующим утверждением: траектории национального дохода (конечного продукта) с темпом rудостижимы, если rу£ l+d. При подстановке (10.32) в (10.37) получаем
![]() (10.39)
(10.39)
Подставляя (10.34) в (10.37), получаем
![]() (10.40)
(10.40)
Введем в функцию Кобба — Дугласа (10.28) временную функцию трудовых ресурсов:
![]()
Проведя преобразования, получаем
![]() (10.41)
(10.41)
Уравнения (10.39) - (10.41) увязывают двухфакторные производственные функции и баланс труда с ростом фондовооруженности труда или объема основных производственных фондов. Поэтому они могут использоваться как однофакторные производственные функции. Однако основное их назначение — включение в более общие макроэкономические модели, в которых k(t) и K(t) являются эндогенными переменными.
Отметим, что соотношение между k(t) и K(t) непосредственно вытекает из определения фондовооруженности труда
K(t)=k(t)L(0)elt(10.42)
Объединим теперь производственную функцию с балансом конечного продукта. С учетом (10.35)
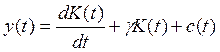 (10.43)
(10.43)
Заменив y(t) двухфакторной производственной функцией общего вида, получаем
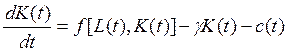 (10.44)
(10.44)
Попытаемся далее совместить выведенные соотношения с принципами регулирования норм накопления, рассматривавшимися в 10.1 — 10.2.
Модель с фиксированной нормой капитальных вложений. Обозначим через а долю капитальных вложений в конечном продукте. Тогда u(t) = ay(t) = af[L(t), K(t)]. Подставляя это выражение в (10.35), получаем
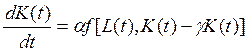 (10.45)
(10.45)
В последующем анализе будем использовать вначале функцию Кобба — Дугласа первой степени, а затем — ее общую форму. Подставив (10.39) и (10.42) в (10.45), получаем
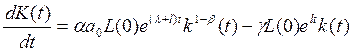 (10.46)
(10.46)
Другое
выражение 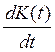 можно получить, дифференцируя (10.42):
можно получить, дифференцируя (10.42):
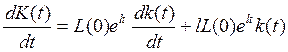 (10.47)
(10.47)
Приравнивая правые части (10.46) и (10.47) и проведя преобразования, приходим к
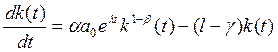 (10.48)
(10.48)
Решением данного дифференциального уравнения является
![]() (10.49)
(10.49)
где h(t) — временна¢я функция, определяемая параметрами k(0), а0, l, a, b, g, l(см. ДМНХ.с. 89).
При
этом 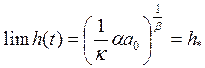
где 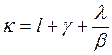
Итак, темп прироста фондовооруженности труда асимптотически приближается к
величине ![]() , асимптотой фондовооруженности является
, асимптотой фондовооруженности является ![]() .
.
Пусть, к
примеру, а0 = 2,5, l = 0,02, l
= 0,01, b = 0,65, g = 0,1, k(0)
= 13,68 тыс. руб. Тогда ![]() = 0,0308, k(5) = 12,92,
= 0,0308, k(5) = 12,92, ![]() (5) = 8,20, k(10) =12,94,
(5) = 8,20, k(10) =12,94, ![]() (10) = 9,56, k(20) = 14,79,
(10) = 9,56, k(20) = 14,79, ![]() (20)
= 13,00. Фактическая и асимптотическая фондовооруженность сближаются.
(20)
= 13,00. Фактическая и асимптотическая фондовооруженность сближаются.
В соответствии с (10.39) и (10.42) получаем
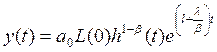 (10.50)
(10.50)
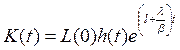 (10.51)
(10.51)
Этим траекториям соответствуют асимптотические траектории ![]() и
и ![]() при
при ![]() . При этом траектория y(t) может находиться как ниже, так и
выше траектории
. При этом траектория y(t) может находиться как ниже, так и
выше траектории ![]() , в зависимости от k(0) и устанавливаемого а.
, в зависимости от k(0) и устанавливаемого а.
Принимая во внимание, что и(t) = ay(t) и с(t) = (1 - а)у(t), приходим к выводу, что динамика основных производственных фондов, конечного продукта и его функциональных элементов стремится к развитию с постоянным темпом прироста rm, являющимся суммой темпа прироста трудовых ресурсов в производственной сфере и асимптотического темпа фондовооруженности труда:
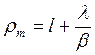 (10.52)
(10.52)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.