Расширенные модели экономического роста, страница 4

Если же k(0) < h_*, то поведение решений качественно различается для Т< Т* (k(0)) и Т*(k(0)) < Т< + .

Когда плановый период короток, а именно Т <Т* (k(0)), тогда неэффективно затрачивать капиталовложения и a*(t) = 0. Решение получается аналогичным рассмотренному выше случаю.

Но если Т> Т*(k(0)), то капиталовложения в начале периода целесообразны, оптимальная норма капиталовложений равна единице. Однако недостаточная длительность планового периода не позволяет довести фондовооруженность до магистрального уровня. По достижении некоторого Т <  (k(0)) норма капиталовложений становится равной нулю и все ресурсы конечного продукта переключаются на потребление. Итак, в этом случае

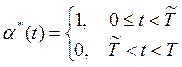
(см. рис. 10.8).

2. (k(0)).

Оптимальная траектория состоит из трех участков: стартового, магистрального, финишного (см. рис. 10.9).

Рис. 10.9. Динамика оптимальной нормы капиталовложений и оптимальной фондовооруженности при :

а) начальная фондовооруженность ниже магистральной; б)начальная фондовооруженность выше магистральной

Использование "автодорожной" терминологии имеет веские основания. Начальный участок — это продвижение к магистрали, на которой можно развить максимальную постоянную скорость. Попав на магистраль, целесообразно проехать по ней возможно большую часть пути (длительности планового периода). Завершающая часть пути — съезд с магистрали для достижения конечной цели движения (максимизация интегрального экономического эффекта).

При tÎ [0, , (k(0))] динамика полностью аналогична рассмотренному выше первому участку развития при Т = ¥. Здесь происходит перестройка структуры распределения конечного продукта с целью приближения фондовооруженности труда к магистральной; при этом характер изменений определяется соотношением исходной и магистральной фондовооруженности. Норма капиталовложений равна либо 0, либо 1.

При tÎ [0, , (k(0)), ] осуществляется магистральное развитие экономики при норме капиталовложений (10.59) и темпе прироста (10.60).

Наконец, на участке tÎ [, T] осуществляется структурная перестройка с целью максимизации потребления. Капиталовложения отсутствуют. На этом участке темп изменения конечного продукта (и потребления) равен r = r(g + l)+l - g. При используемых исходных данных r = — 0,0085.

Проблема "хвоста" планового периода сохраняется в том смысле, что уменьшение фондовооруженности труда и объема основных производственных фондов не учитывает интересы послепланового развития. Чтобы ослабить этот недостаток, целесообразно вводить в модель некоторые ограничения на конечные состояния, например ,  т.п.

Важно отметить, что при  продолжительность стартового и финишного участков не зависит от Т. С увеличением Т все большая часть траектории проходит по магистрали. Поэтому анализируемая модель особенно привлекательна для долгосрочного прогнозирования и планирования. Главной особенностью оптимальной траектории является магистральный участок развития, на котором поддерживаются постоянными максимально возможный темп и основные макроэкономические пропорции. Исключаются релейные переключения потребления и накопления, а также чрезмерная зависимость поведения решения от Т. При достаточной длительности планового периода "переходные" этапы с резкими структурными сдвигами занимают относительно небольшую часть траектории. Кроме того, для финишного участка легко применяются сглаживающие регуляторы.