Расширенные модели экономического роста, страница 3

Оптимизация с переменной нормой капитальных вложений. Рассмотрим задачу максимизации дисконтированного потребления на одного работника производственной сферы за период [0, 7]:

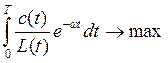                          (10.58)

Эта целевая функция дает почти те же результаты, что и максимизация дисконтированногопотребления на душу населения, но при этом упрощает формулы расчетов.

Функция c(t) выражается через y(t) по формуле (10.50), которая включает экспоненциальный множитель с темпом 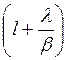. После преобразований (10.56) входящий в нее экспоненциальный множитель получает темп 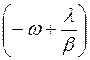 в дальнейшем принимается обозначение: 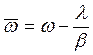. В анализе решения важную роль играет число , определяемое параметрами а₀, b, ,  и расчетные отрезки времени (k(0)), Tt, , T*(k(0)), также определяемые параметрами модели[2]. При подстановке введенных ранее исходных данных имеем = 0 05,  = 0 14, = 10,6, =1,83,  = 7,46.

В 10.2 было показано, что оптимальное решение задачи с переменной нормой накопления, но постоянной капиталоемкостью сильно зависит от продолжительности планового периода. При небольшом накопление вообще отсутствует, а при достаточно большом Т оптимальная траектория содержит релейное переключение потребления и накопления. Логично предположить, что введение в модель переменной капиталоемкости, регулируемой с учетом условий оптимизации, должно способствовать получению более гладких и устойчивых оптимальных решений.

Оптимальная стратегия развития по анализируемой модели зависит от величины T и начального уровня фондовооруженности k(0). Вначале рассмотрим стратегию развития при допущении, что плановый горизонт бесконечен: Т =¥.

Бесконечная траектория экономического развития состоит из двух участков (см. рис. 10.7).

Рис. 10.7. Динамика оптимальной нормы капиталовложений и оптимальной фондовооруженности труда на бесконечном интервале времени: а) начальная фондовооруженность ниже магистральной; б) начальная фондовооруженность выше магистральной/

При tÎ[0, ] оптимальная норма капиталовложений принимает только одно из двух значений: 0 или 1. Если k(0) < , то требуется максимально быстро поднять фондовооруженность, поэтому a*(t) = 1 (рис. 10.7). Если же k(0) > , то, наоборот, в интересах максимизации потребления не следует затрачивать капиталовложения, поэтому a*(t) = 0, а фондовооруженность снижается (рис. 10.7). В этом случае объем основных производственных фондов уменьшается (поскольку отсутствует возмещение выбытия фондов), а объем конечного продукта изменяется темпом r = l + lb + gb -g. При используемых исходных данных это дает r_у — — 0,0085.

Рис. 10.8. Динамика оптимальной нормы капиталовложений и оптимальной фондовооруженности при продолжительности планового периода и начальной фондовооруженности ниже магистральной.

При t>  должна поддерживаться постоянная норма капиталовложений

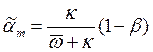         (10.59)

представляющая собой модификацию "золотого правила накопления". При использовании прежних исходных данных получим  = 0,247. В точке t =  траекториявыходит на магистраль с постоянным темпом прироста конечного продукта, потребления, капиталовложений и основных производственных фондов:

При используемых исходных данных  = 0,0408. Фондовооруженность, так же как и производительность труда, растет темпом  = 0,0308.

Перейдем к анализу динамики экономического развития при ограниченной продолжительности планового периода Т<¥. Здесь принципиально важны два случая.

1.

Оптимальная норма- капиталовложений может принимать только два значения: 0 или 1.

При k(0) > h_*исходный уровень фондовооруженности достаточно высок и поэтому при небольшом плановом горизонте капиталовложения нецелесообразны: а_* (t) = 0 для всех t Î [0, Т]. Траектория аналогична первому участку развития при бесконечном периоде, когда k(0) > (см. рис. 10.7).