Расширенные модели экономического роста, страница 2

Существенным отличием полученного результата от решения модели с постоянной нормой накопления (10.11) является то, что темп r_mне зависит от нормы производственных капитальных вложений. Однако эта норма положительно влияет на рост фактического конечного продукта y(t) через множитель h¹ - b(t). При использованных выше исходных данных r_m= 0,0408. В диапазоне нормы производственных капиталовложений аÎ[0, T] имеем y(t) >.

Проанализированная ситуация экономического роста с фиксированной нормой производственных капиталовложений известна в литературе как модель Солоу, или Солоу - Свена (см. комментарий в ДМНХ, с. 91 - 92).

Для большей сопоставимости полученных выводов с моделью, излагавшейся в 10.1, перейдем к формулам национального дохода, используя (10.50) - (10.52):

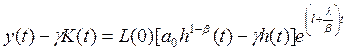(10.53)

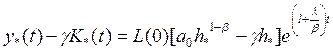        (10.54)

Полученные траектории качественно не отличаются от траекторий конечного продукта.

Отметим особые свойства модели, включающей функцию Кобба — Дугласа при . Используя аналогичные приемы математического анализа, что и для функций первой степени, получаем решение в виде

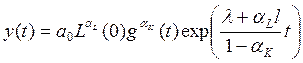(10.55)

При 0 < а_K < 1 динамика y(t) аналогична динамике в (10.50). Темп прироста конечного продукта стремится к темпу

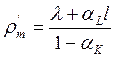
Другие свойства фактической и асимптотической траекторий развития при 0 < а_K< 1 качественно также не отличаются от результатов анализа при a_L= b, а_к = 1 — b, 0 < b < 1. Однако при а_к > 1 модель приобретает качественно иные свойства (см. ДМНХ, с. 92).

Оптимизация с постоянной нормой капитальных вложений. Логическим развитием рассмотренной выше модели является оптимизация постоянной нормы производственных капитальных вложений. При этом, как и в 10.2, максимизируется суммарное потребление за любой промежуток времени (в том числе и дисконтированное потребление).

Ввиду того, что анализ модели требует довольно длинных математических выкладок, ограничимся экономической интерпретацией конечных результатов (более подробное изложение см. в ДМНХ, с. 93 - 94).

Постоянной норме капиталовложений а_т = 1-b соответствуют траектории конечного продукта, потребления, капиталовложений и основных производственных фондов, имеющие одинаковый постоянный темп прироста r_m= . Экономическое развитие с неизменной структурой и наивысшим темпом роста принято называть магистральным, а соответствующую траекторию — магистралью.

Итак, оптимальная норма а_т при магистральном развитии равна эластичности конечного продукта по основным производственным: фондам[1]. Такое определение известно как “золотоеправило накопления" (впервые этот результат получил Е.Фелпс).

Для немагистральной траектории роста потребления норма а_т = 1—b в общем случае не является оптимальной. Оптимальная норма а* должна обеспечивать максимум суммарного или дисконтированного потребления за плановый период [0, Т]:

а) 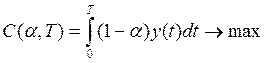, aÎ[0, 1]      (10.56)

б), 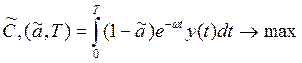, aÎ[0, 1],       (10.57)

где у(t) определяется из (10.50).

Отметим два свойства оптимальных норм капиталовложений а* и , являющихся решением (10.54), (10.55).

1. Чем продолжительнее плановый период [0, Т], тем больше оптимальная норма а* для данного периода соответствует магистральной а_т= 1-b;

2. Чем выше дисконт потребления w > 0, тем меньше .

В соответствии с приведенными выше исходными данными „магистральная норма а_т = 0,35. Приведем расчеты оптимальных норм а*(Т) и при разной продолжительности планового периода и дисконте потребления w — = 0.08:

а* (5) = 0, а* (10) = 0,02, а* (20) = 0,21.

а*(5) = 0. а*(10)= 0, а*(20) = 0,16.

Решения проанализированной модели обладают существенными преимуществами по сравнению с решениями моделей из 10.2, в которых оптимальная норма накопления гораздо сильнее зависит от продолжительности планового периода и не стремится к какому-либо устойчивому уровню внутри отрезка [0, 1] .