Временной ряд. Оценка логистической функции. Стационарные модели

Талышева Любовь Пантелеевна

ЭКОНОМЕТРИЯ-2

Лектор: Талышева Любовь Пантелеевна

Оформление: Лосева С.С. & Комаристый Е.Н.

Ó Copyright1997

ЛЕКЦИЯ 1

Последовательность наблюдений (существенность порядка, в котором следуют эти наблюдения) называется временным рядом (ВР).

Временной ряд непрерывный, если время измеряется непрерывно.

Временной ряд дискретный, если время измеряется дискретно. В зависимости от способа получения измерений дискретности имеем:

·  моментальный ВР

·  интервальный ВР

Моментальный временной ряд - выборка из непрерывного временного ряда. Пример - численность населения.

Если временной ряд получен в результате накопления значения элементов, то это интервальный временной ряд. Пример - динамика выпуска продукции.

Детерминированный временной ряд, если будущее значение точно описывается какой-либо математической функцией.

Если временной ряд может быть получен только с помощью распределения вероятности, то это случайный временной ряд. Случайный временной ряд - это лишь одна частная реализация стохастического (развивается во времени согласно законам теории вероятности) процесса. В каждый момент времени t наблюдения . Всякий временной ряд полезно рассматривать как смесь, совокупность нескольких компонент:

·  тренд - долговременная статистическая составляющая, главная, ведущая все изменения;

·  периодическая составляющая (в частности - сезонная);

·  нерегулярная (кратковременная, систематическая) составляющая;

·  случайная компонента.

Если их объединить: , где - детерминированная составляющая, а - белый шум.

Существует несколько разновидностей тренда:

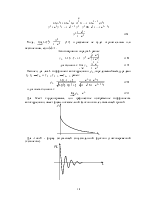
Стационарный процесс - процесс, который находится в определенном статистическом равновесии.

Если совместное распределение вероятностей точек случайной величины инвариантно по отношению к общему сдвигу временного аргумента, т. е. совместное распределение случайных величин в моменты времени  точно такое, как совместное распределение  в моменты времени для любых k, то процесс строго стационарен.

Условно ВР (временной ряд) можно считать  стационарным, если неизмененными во времени являются моменты первого и второго порядка.

Мы будем иметь дело со слабо стационарными процессами.

Стационарность второго порядка.

- неизменна дисперсия

- автоковариация неизменна

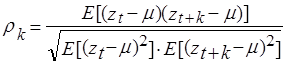 в случае стационарност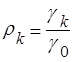и

 и  не зависят от t а зависят только от k.

Вид ковариационной матрицы для стационарного процесса (m измерений в течение n периода времени: - наблюдения):

.

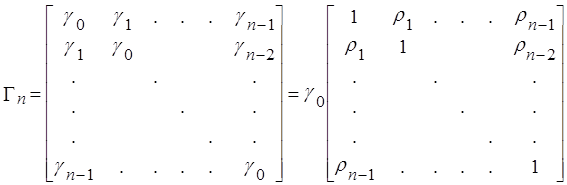Автокорреляционная функция - последовательные значения коэффициентов автокорреляции.

Само понятие тенденции не является строгим. Виды тенденций:

1)  Полиномиальный тренд. Описывается с помощью полинома: 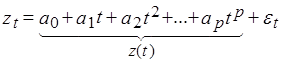,          (1)                                          

2)  Экспоненциальный тренд. , где - “белый шум” - нерегулярная компонента.

3)  Гармонический тренд (см. спектральный гармонический анализ)

4)  Логистическая кривая.

Для 1 и 2 легко строится регрессия. Когда подбираем тенденцию возникает вопрос: на какой степени остановиться? Если полином с низкой степенью, то есть опасность смешения, с другой стороны, если увлечься подробностью, то не подходит минимальность дисперсии. Где золотая середина? Критерием выбора степени полинома может служить стационарность остатков, полученных после исключения тренда.

МЕТОД СКОЛЬЗЯЩИХ (подвижных) СРЕДНИХ.

При выборе полинома высоких степеней имеем риск “качнуть хвост”.

Выбираем отрезок скольжения из нечетного числа точек (2m+1). Подбираем для него полином (1), находим параметры полинома, находим значение среднего, затем для 2…2m+2 находим значение этого полинома, оцениваем с помощью среднего. Нет необходимости каждый раз оценивать полином. Пользуемся методом наименьших квадратов:

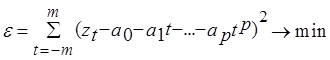    (2).

Находим частные производные по  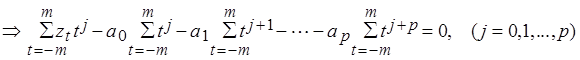    (3) .

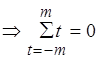Если t=0, то наша задача заключается в том, чтобы найти только один параметр , что будет зависеть от m и p.

Пример.

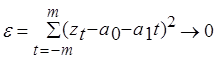
Первая частная производная: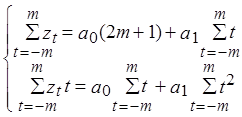

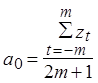
Пусть p=2, m=2, тогда 2m+1=5, т.е. по пяти точкам.

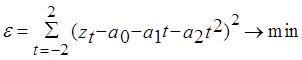
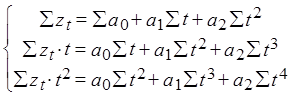
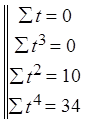
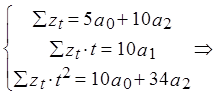
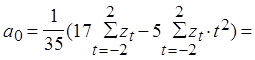
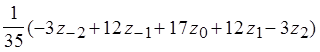-среднеквадратичное значение.

Свойства скользящих средних:

1. Сумма весов  равна

Доказательство:

Т.к.  зависят только от p и m, то можно записать так: пусть  для любого t. Нужны уравнения с нечетными степенями t, тогда система (3) преобразуется следующим образом:

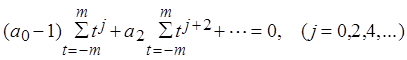
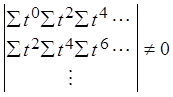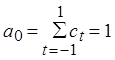, значит , следовательно - это мы доказали в частном случае.

2.

Это следует из того, что они получаются как функции сумм: 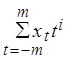, которые сами симметричны.

3. Для полиномов четного порядка (р=2k) формулы будут теже самые, что и для полиномов нечетного порядка (p=2k+1). Пусть p=2k+1, тогда матрица коэффициентов системы (3) при неизвестных параметрах  будет выглядеть следующим образом: