Задания на контрольную работу по дисциплине "Эконометрия" (Варианты 1-2 по 6 вопросов)

1. Найдите скорректированный  в регрессии , построенной по 24 наблюдениям, если сумма квадратов центрированных значений x равна 230, а сумма квадратов остатков равна 100.

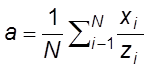2. Рассмотрите уравнение регрессии без константы . Предполагается, что выполнены стандартные предположения модели линейной регрессии. Рассмотрите следующую оценку для коэффициента α: . Докажите, что a является несмещенной оценкой величины α. Найдите дисперсию этой оценки. Является ли эта оценка линейной? Поясните.

3. Мат. ожидание величин x₁ и x₂ одинаково и отличается от мат. ожидания величин x₃ и x₄ на некоторую константу. Как эту ситуацию можно описать моделью линейной регрессии с фиктивными переменными? Запишите зависимую переменную и матрицу факторов.

4. Качественный фактор имеет 2 уровня: A и B, и a_i, b_i — соответствующие фиктивные переменные. Была построена регрессия, включающая некоторый количественный фактор z_i и не включающая переменную для A: x_i = 102 – 0,77z_i + 21b_i + e_i. Найдите оценки для регрессии, включающей обе фиктивные переменные, с ограничением, что сумма коэффициентов при фиктивных переменных равна нулю.

5. Переменные регрессии были подвергнуты преобразованию в пространстве наблюдений с помощью матрицы D = diag{1,2,…,N}. При этом оказалось, что ошибки в преобразованной регрессии удовлетворяют всем обычным предположениям модели регрессии. Какую структуру имела матрица корреляций ошибок в первоначальной регрессии?

6. Ошибка e_i в регрессии с N=50 наблюдениями описывается авторегрессией первого порядка. Статистика Дарбина—Уотсона оказалась равной 0,6. Оцените корреляцию между ε₂₁ и ε₂₃.

1. Ошибка e_i в регрессии с N=100 наблюдениями описывается авторегрессией первого порядка. Статистика Дарбина—Уотсона оказалась равной 2,4. Оцените корреляцию между ε₃₃ и ε₃₆.

2. Переменные регрессии были подвергнуты преобразованию в пространстве наблюдений с помощью матрицы D = diag{1,1/2,…,1/N}. При этом оказалось, что ошибки в преобразованной регрессии удовлетворяют всем обычным предположениям модели регрессии. Какую структуру имела матрица корреляций ошибок в первоначальной регрессии?

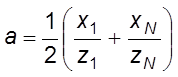3. Рассмотрите уравнение регрессии без константы . Предполагается, что выполнены стандартные предположения модели линейной регрессии. Рассмотрите следующую оценку для коэффициента α: . Докажите, что a является несмещенной оценкой величины α. Найдите дисперсию этой оценки. Является ли эта оценка линейной? Поясните.

4. Качественный фактор имеет 2 уровня: C и D, и c_i, d_i — соответствующие фиктивные переменные. Была построена регрессия, включающая некоторый количественный фактор z_i и не включающая переменную для C: x_i = –14 – 0,37z_i + 43d_i + e_i. Найдите оценки для регрессии, включающей обе фиктивные переменные, с ограничением, что сумма коэффициентов при фиктивных переменных равна нулю.

5. Мат. ожидание величин x₁, x₃ и x₄ одинаково и отличается от мат. ожидания величин x₂ и x₅ на некоторую константу. Как эту ситуацию можно описать моделью линейной регрессии с фиктивными переменными? Запишите зависимую переменную и матрицу факторов.

6. Найдите скорректированный  в регрессии  построенной по 20 наблюдениям, если сумма квадратов центрированных значений x равна 95, а  сумма квадратов остатков равна 25.