Временной ряд. Оценка логистической функции. Стационарные модели, страница 4

Если теперь подставить в эту формулу t=12, то получим предсказание для численности шведского населения на 1960г.                     ()

1	10				0,1
2	13	0,3	1,35	- 1,03	0,071	0,1
3	15	0,15	1,17	- 1,77	0,067	0,071
4	16,5	0,1	1,07	- 2,66	0,061	0,067
5	17	0,03	1,036	- 3,32	0,059	0,061

Логистическая кривая I способ:

ЛЕКЦИЯ 3.

СТАЦИОНАРНЫЕ МОДЕЛИ

Некоторые простые операторы. Оператор сдвига назад B рассматривается как

,

отсюда:

Модель линейного фильтра. Временные ряды, в которых последовательные значения сильно зависимы, целесообразно рассматривать как генерируемые последовательностью независимых импульсов . Эти импульсы - реализация случайной вероятности с фиксированным распределением, которое обычно предполагается нормальным с нулевым средним и дисперсией .

Т.к. случайные переменные нескорелированны, то автоковариационная функция должна иметь вид:

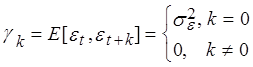
Таким образом автокорреляционная функция имеет очень простую форму:

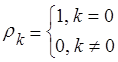
Такой процесс называют в статистике чисто случайным процессом, а последовательность случайных величин  в технической литературе белым шумом.

Предполагается, что белый шум  можно трансформировать в процесс  при помощи линейного фильтра:

Это представление временного ряда как выхода линейного фильтра. Операция линейной фильтрации заключается в вычислении взвешенной суммы предыдущих наблюдений, так что

                                                 (1)

где m - параметр, определяющий “уровень процесса”, а  - линейный оператор, преобразующий  в  и называемый передаточной функцией фильтра.

Последовательность , образованная весами, теоретически может быть конечной или бесконечной. Если эта последовательность (конечная или бесконечная) сходится, фильтр называется устойчивым, а процесс  будет стационарным. Параметр m будет тогда средним, вокруг которого процесс варьирует. В другом случае процесс  нестационарен и m не имеет какого-либо особого смысла, кроме как некой точки отсчета уровня процесса.

МОДЕЛЬ АВТОРЕГРЕССИИ

В этой модели текущее значение процесса выражается как конечная линейная совокупность предыдущих значений процесса и импульса .

Обозначим через  отклонение  от m, т.е.

,

тогда

                                                                  (2)

Называется процессом авторегрессии (АР) порядка p.

,

или

Если мы определили оператор авторегрессии порядка p как

,

то модель авторегрессии можно сжато написать как

                                                                                                          (3)

Эта модель содержит (p+2) неизвестных параметра: , которые на практике следует оценить по наблюдениям.  - дисперсия белого шума.

Нетрудно заметить, что модель авторегрессии является частным случаем (видом) модели линейного фильтра. Например,  можно исключить из правой части (2) подстановкой

Аналогичным образом можно исключить  и т.д. , получив в результате бесконечный ряд из e.

Символически это можно записать так:

,

где .

Процессы авторегрессии могут быть стационарными и нестационарными. Чтобы процесс был стационарным, необходимо выбрать веса j так, чтобы веса  образовывали сходящийся ряд.

МОДЕЛИ СКОЛЬЗЯЩЕГО СРЕДНЕГО

Модель авторегрессии (2) выражает отклонение  процесса в виде конечной взвешенной суммы p предыдущих отклонений процесса  плюс случайный импульс . Равным образом, как было показано, она выражает  как бесконечную взвешенную сумму e.

Другой тип моделей, имеющих большое значение в описании наблюдаемых временных рядов, - это так называемый процесс скользящего среднего, когда  линейно зависит от конечного числа q предыдущих e.