Временной ряд. Оценка логистической функции. Стационарные модели, страница 5

Такой процесс

                                                                    (5)

называется процессом скользящего среднего (СС) порядка q. Название “скользящее среднее” слегка вводит в заблуждение, т.к. веса , на которые умножаются e, не обязаны давать в сумме единицу, или хотя бы быть положительными. Однако из-за общеупотребительности этого термина мы будем его придерживаться.

Если мы определим оператор скользящего среднего порядка q как

                                      ,                                    (6)

то модель скользящего среднего можно сжато записать так:

                                                                                                               (7)

Она содержит q+2 неизвестных параметра: , которые способны оцениваться по наблюдениям. Отсюда следует, что процесс скользящего среднего можно трактовать как выход  линейного фильтра с передаточной функцией , на выход которого поступает белый шум .

Рассмотрим модель:

                                                                                      (8)

в которой  при j>1. Выражая через , получим:

,

отсюда:

и, выражая отклонения  через прошлые отклонения, получим:

                                                                  (9)

Т.е. конечный процесс скользящего среднего может быть записан как бесконечный процесс авторегрессии. Поэтому, если процесс действительно типа СС(1), его представление в виде процесса авторегрессии невозможно. Аналогично процесс АР(2) не может быть экономично представлен с помощью скользящего среднего.

На практике для получения экономичной параметризации иногда бывает необходимо включить в модель как члены, описывающие авторегрессию, так и члены, моделирующие скользящее среднее.

Такой процесс:

                                             (10)

или:

                                                                                                      (11)

Называется смещенным процессом авторегрессии скользящего среднего порядка (p, q), и иногда сокращенно обозначается нами АРСС(p, q). Например, процесс авторегрессии - скользящего среднего порядка (1, 1) АРСС(1, 1) имеет вид:

                                                                                           (12)

Т.к. (11) можно записать в виде:

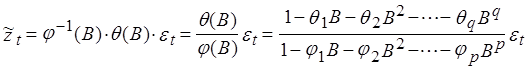               ,           (13)

Смешанный процесс авторегрессии - скользящего среднего можно интерпретировать как выход  линейного фильтра, передаточная функция которого есть отношение двух полиномов, на вход которых подается белый шум e.

АВТОРЕГРЕССИОННЫЙ ПРОЦЕСС ПЕРВОГО ПОРЯДКА

                                                                                                            (14)

или ПРОЦЕСС МАРКОВА

,т.к.

                                                                      (15)

то рассмотрение такого процесса будет равно

с

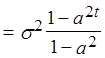                                                                                                                (16)

Тогда, 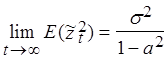  (17) и рассеяние не будет отрицательным или бесконечным, если .

Автоковариации порядка L равны:

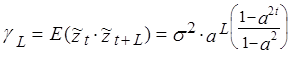                                                                            (18)

                                            для больших t: 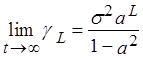                                    (19)

Наконец, для лага L коэффициент автокорреляции , определяемый между рядами  и  равен:

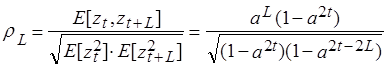                                                         (20)

и для очень больших t:

                                                                                                                 (21)

Для 0<a<1 коррелограмма, или графическое изображение коэффициента автокорреляции, имеет форму показательной функции в виде убывающей кривой.

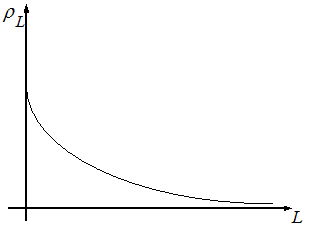
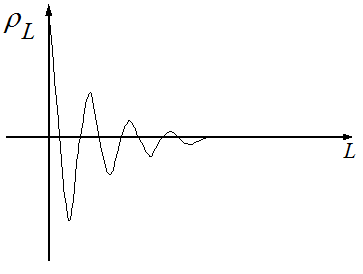
Для -1<a<0 - форму затухающей синусоидальной функции (знакопеременной экспоненты).