Временной ряд. Оценка логистической функции. Стационарные модели, страница 2

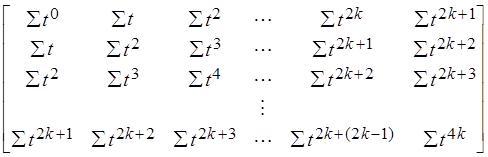
Для нахождения  нам нужно рассмотреть уравнение с четными степенями t(1-e, 3-e,…). Сумма с нечетными степенями t всегда равна нулю. Последняя строка не будет участвовать.

Формулы не позволяют вычислить значение тренда для первых m и последних m точек. Хотя в начале отсутствие этих точек и не страшно, но в конце - нежелательно. Для получения последних m точек надо решить систему (3), но при этом веса для не будут симметричны, т.е. в сумме не равны 1.

Предостережение: сглаживание временного ряда при использовании метода скользящих средних уменьшает значимость случайной составляющей. С другой стороны для чисто случайных последовательностей метод приведет к асциллирующей последовательности. Что это значит? Если при помощи метода изучаются циклические составляющие, то использование этого метода кроме систематических колебаний может привести к получению искусственных колебаний, вызванных этим методом. Это так называемый эффект Слуцкого.

Практические рекомендации: автокорреляционная функция - последовательность значений автокорреляции , которые представляют собой зависимость от величины задержки (величины лага). Это также называется коррелограммой. Как поступают в конкретных случаях: если процесс стационарный, то 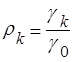. Эмпирически считается с использованием двух способов: теоретический коэффициент автокорреляции - , и эмпирический: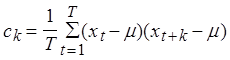, где 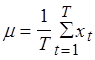. Иногда в формуле деление осуществляют не на Т, а на (T-k), что предпочтительнее.

При построении эмпирической автокорреляционной функции для обеспечения необходимой точности теоретической автокорреляционной функции как правило используют следующие ограничения для величины задержки k. Величину k ограничивают 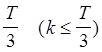. Иначе не обеспечивается достаточная надежность.

Как проверить наличие тенденции у ВР?

Тренд средних: критерий проверки существования тенденции:

1.  Пусть имеется временной ряд  (с возрастающей тенденцией), упорядоченный во времени.

2.  Можно упорядочить все  по возрастанию .

Сравниваем 1) и 2).

Для чисто случайного процесса  и  не будут между собой связаны, а при наличии тенденции они коррелируют.

Существует ранговый коэффициент корреляции Спирмена – частный случай парного коэффициента корреляции.

 - ранг, присваиваемый наблюдению  при новом порядке, таким образом,

коэффициент Спирмена: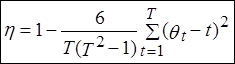

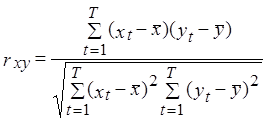 - чисто случайных процессов  имеет  и .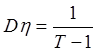

Для больших выборок распределение  нормальное: 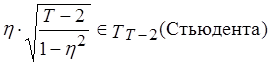, следовательно, можно использовать критерий Стьюдента.

Выведем  и  :

,

 - последовательность во времени;

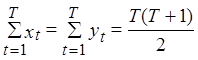 - последовательность по возрастанию.

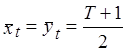
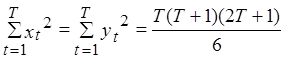
 - разница в рангах

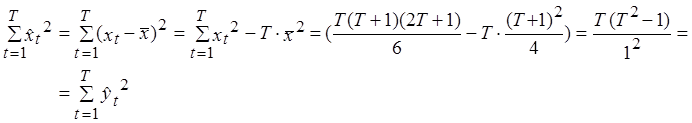
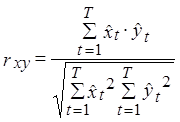
Выразим числитель. Для этого:

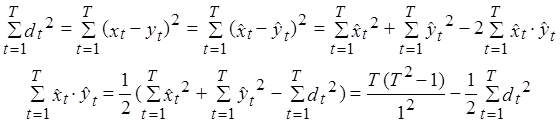
Отсюда .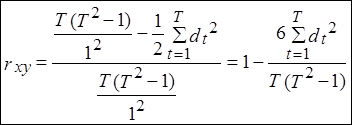

ЛЕКЦИЯ 2.

ОЦЕНКА ЛОГИСТИЧЕСКОЙ ФУКЦИИ

Логистической кривой иногда пользуются для представления роста населения. В эконометрии ее можно часто рассматривать как тенденцию экономических временных рядов, связанных с населением.

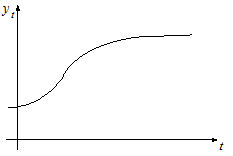
Проще применять тенденцию, состоящую из степеней переменных, выражающих время, или же такую тенденцию, которая являлась показательной функцией относительно времени. Но у таких тенденций неприятное свойство - становиться бесконечными с течением времени. Итак, они, возможно, годяться для интерполяции временных рядов, но вряд ли для их экстраполяций.

И наоборот, логистическая кривая имеет свойство стремиться, при нарастании времени, к асимптоте. Определение логистической функции будет:

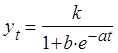                                                         (1)

где t - время, k, a, b - постоянные, в общем неизвестные. Постоянная k является верхней асимптотой логистической кривой. Ясно видно, что:

                                                               (2)

Следовательно k будет наибольшим значением, которое может принять логистическая функция.