В этой системе уравнений четыре неизвестных тока и четыре потокосцепле-ния. Для решения системы следует электромагнитные переменные выразить либо через потокосцепления, либо через токи. Выразим потокосцепления через токи, пля чего спроецируем векторы потокосцеплений (1.11) на координатные оси:
где все величины записаны в координатах статора
Учитывая,
что dQ/dt= со, систему (1.8) перепишем в неподвижных координатах
статора: 
Поскольку корректность математических моделей не зависит от
выбора координатных осей, но вид координат может упростить анализ, обычно в
зависи мости от объекта и задач исследования выбирают одну из трех координатиьп
систем: неподвижную (1.9), синхронно вращающуюся в пространстве со ска ростью
поля статора или вращающуся со скоростью ротора [16]. Чтобы прив■•■ сти
уравнение (1.9) к координатам, вращающимся в пространстве в общем cjry1 чае с произвольной скоростью сок,
можно воспользоваться тем же приемом, до|
множив переменные векторы на оператор поворота в *, где 6* — угол межд
Учитывая симметрию асинхронной машины по осям (LMd = LM = LM; Lsd=
= Lsq = Ls-tLrd = Lrq—Lr) и подставив (1.13) в (1.12), запишем систему отно--ительно токов [11]:
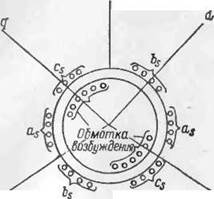
на рис. 1.7. В этой модели параметры обмоток фаз соответствуют параметрам фаз исходной трехфазной модели кроме взаимной индуктивности £д, которая ь 3/з раза больше взаимной индуктивности фазы трехфазной системы. Здесь в уста новившемся режиме переменные соответствующих фаз являются периодическим! функциями- времени с временным сдвигом между соответствующими переме | нкми различных фаз 90° и с угловыми частотами статорных величин сок — cos роторных сок — со.
1.2. Модели электромеханическихпреобразователей свозбуждениемоднойизчастей постояннымтоком
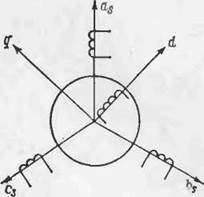
Электромеханические преобразователи (ЭМП) такого тип; имеют две модификации: с возбуждением ротора постоянным током и с возбу-.' дснием статора постоянным током. Наиболее распространенной технической per лнзацией первой модификации является синхронный двигатель. Будем полагать что синхронный двигатель имеет трехфазную обмотку на статоре и неявнополк.; ный ротор с двумя полюсами, а успокоительные обмотки отсутствуют. Первичная модель такого ЭМП приведена на рис. 1.8. В отличие от асинхронных ма шин здесь координатную ось dобычно жестко связывают с ротором и ориг i тируют по оси полюсов. Это естественно и удобно, поскольку при возбуждена ротора постоянным током ось магнитного потока, возбуждаемого обмоткой р тора, неподвижна относительно ротора. В остальном в технической литературе физические величины рассматриваемых ЭМП обозначаются по-разному. Поэтому за основной принцип при выборе обозначений примем, как в аси хронных машинах, принадлежность переменных и параметров статору либо ротору .
Тогда для рассматриваемой модели можно записать систему уравнений р& а новесия напряжений, аналогичную
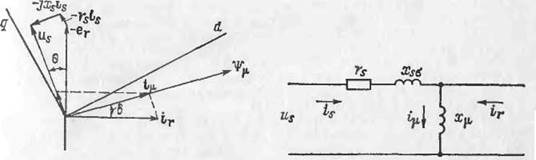
где в отличие от (1.3) индексом / обозначены переменные и параметры обмоток возбуждения на роторе.
Поскольку в неявнополюсном синхронном двигателе воздушный зазор можно считать равномерным, то уравнениям (1.15) соответствует катушечная моде iЭМП, подобная модели асинхронной машины (см. рис. 1.3), с тем различием, что здесь на роторе расположена однофазная обмотка. В этой модели по осям фаз статора расположены сосредоточенные катушки, эквивалентные фазным обмоткам, а по оси dротора — обмотка возбуждения ротора. Так же ка и для асинхронной машины, можно изобразить переменные фазные величины ста тора в виде временных векторов, пульсирующих по осям фаз, и, сложив их rei метрически, построить систему пространственных векторов статора. Для постро ния полной векторной диаграммы необходимо параметры обмотки ротора прит;к сти к обмоткам статора [16], например ток
Рассмотрим особенности функциональных схем, обусловленные неполной управляемостью тиристоров и спецификой дискретного управления переменными.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.