Поведение каждой из перемениых исходной (приближенной к реальной конструкции) модели (рис. 1.2) может быть описано как изменение во времени эквивалентных векторов переменных, направленных по осям фаз. Такому описанию соответствует эквивалентная модель машины, где реальные обмотки заменены эквивалентными сосредоточенными катушками, расположенными по осям фаз (рис. 1.3) и обладающими параметрами обмоток фаз [1, 17]. Для каждой фазы такой модели соотношение перемениых удобно показать на векторной диаграмме [7, Ю], построенной для произвольной фиксированной частоты с учетом принятых ранее допущений (рис. 1.4). Кроме того, при построении векторной диаграммы параметры ротора были приведены к параметрам статора, а диаграмма построена для иксированного момента времени, когда вектор фазного напряжения совпадает с осью фазы при вращении векторов против часовой стрелки. Эта диаграмма представляет собой своего рода математическую абстрактную модель, основанную на известном в электротехнике приеме изображения гармонических функций в виде вращающихся временных векторов. Реальные временные соотношения между переменными фазы определяются проекциями вращающихся векторов на ось фазы, а временные фазовые сдвиги между переменными соответствуют углам между векторами. Следует отметить, что для упрощения диаграмма построена для машины, возбуждаемой только со стороны статора, при возбуждении же обеих частей ЭМП вектор тока ротора будет определяться еще н
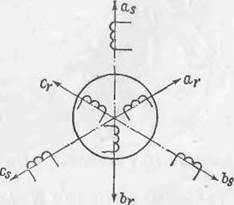
Рис 1.3. Эквивалентная катушечная модель асинхронной машины
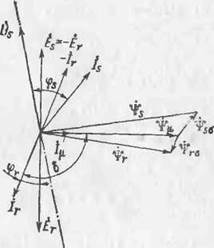
Рис. 1.4. Векторная диаграмма фазы асинхронной машины
напряжением, приложенным к фазе ротора, н может быть ориентирован иначе, о чем будет сказано позже.
Все векторы на диаграмме соответствуют реально существующим переменным, кроме намагничивающего тока /ц. Этот ток определяет по модулю и фазе часть тока статора (или ротора), которая, проходя через обмотку с индуктивностью, равной взаимной индуктивности фаз статора и ротора L^, создает в
воздушном зазоре ЭМП рабочее потокосцепление Ч'ц. Полное же потокосцепление каждой катушки (см. рис. 1.3) определяется суммой рабочего потокосцеп-ления и потокосцеп.пения рассеяния (Ф^ или Ч5^). Поскольку потокосцепления определяются совокупным действием всех токов, то для мгновенных значений переменных фазы можно записать:
Здесь Lg = L|( + Lga; Lr = L^ + Lra; Ls, Lf— полные индуктивности фазы ci j гора и ротора соответственно; Lg(fLra— индуктивности рассеяния соответствующих фаз; L^ взаимная индуктивность фаз статора и ротора, причем L
в трехфазных машннах благодаря взаимному влиянию всех трех фаз в % раза больше взаимной индуктивности фазы статора и ротора при их соосиом расположении [16].
Поскольку рабочее потокосцепление является общим для обмоток как статора, так и ротора, то на основании (1.4), раскрывая полные индуктивности, можно записать для каждой фазы:
Так как без учета активной составляющей тока холостого хода /, + tr/ц, получим
Таким образом, рабочее потокосцепление можно выразить непосредственно через сумму токов статора и ротора:
Под действием рабочих потокосцеплений обмоток всех (в нашем случае трех) фаз машины в воздушном зазоре формируется вращающееся магнитное поле, которое можно описать вращающимся эквивалентным пространственным вектором в плоскости, перпендикулярной оси вала [11, 16]. Учитывая, что переменные величины описываются временными векторами, пульсирующими по осям фаз (рис. 1.3), примем за начало отсчета времени момент прохождения рабочего потокосцепления фазы а через нулевое значение. Тогда для мгновенных значений рабочих потокосцеплений фаз можем написать:
Считаем машину двухполюсной, что общепринято при построении математических моделей [1, 11, 16]. В этом случае угловая частота сети <os будет соответствовать угловой скорости магнитного поля в воздушном зазоре и, соответственно, синхронной скорости ротора. Задав вначале cos< = 0 и для простоты построений приняв 4^=1, из (1.7) получим f^ = 0; «F^ = -^/2; ^с=.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.