= д/3~/2. Учитывая, что рабочие потокосцеплення фаз ориентированы по осям фаз, и сложив их геометрически, получим результирующий пространственный вектор Ч'ц для момента времени a>st = 0 (рис. 1.5). Проделав ту же операцию для ряда последовательных значений cos/ ((Ast = 60° и т. д.), можно показать, что результирующий пространственный вектор каждый раз будет поворачиваться на угол Дш*/, а его амплитуда будет ^/гЧ^т (рис. 1.5), т. е. пространственный вектор будет вращаться со скоростью a>st, а его амплитуда в 3/г раза больше модуля соответствующего временного вектора фазы.
Таким же образом мы можем получить результирующие пространственные векторы всех электромагнитных переменных машины Поскольку при формировании результирующих векторов геометрически складываются соответствующие временные векторы, ориентированные в пространстве по осям фаз и имеющие
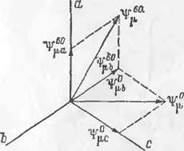
Рис. 1.5. Построение результирующего пространственного векторд
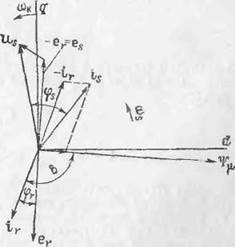
Рис. 1.6. Пространственная вектор пая диаграмма асинхронной машины
одинаковые фазовые сдвиги относительно других временных векторов собствен ной фазы, конфигурация пространственной векторной диаграммы машины буде такой же, как и временной диаграммы фазы. На рис. 1.6 приведена простраи ствениая векторная диаграмма асинхронной машины при ее возбуждении тольк со стороны статора. Поскольку характеристики ЭМП определяются изменением амплитуд и взаимной ориентацией векторов переменных, на рис. 1.6 начальна фаза векторов выбрана произвольно относительно координатных осей d, q[16 17], причем эти оси вращаются в пространстве с угловой скоростью сок. Кром того, пространственный угол б между результирующими векторами рабочего по токосцепления и тока ротора по аналогии с синхронными машинами будем на зывать углом нагрузки.
В технической литературе координатным осям присваивают различные об значения в зависимости от скорости их вращения, привязки к различным чаетт -ЭМП либо начальной их фазировки. Это затрудняет анализ и требует держа в памяти все системы обозначений. Поэтому здесь и далее принята единая c;i стема обозначений координатных осей для этих типов ЭМП: d— продольная ось, q— поперечная ось. Привязка же этих осей к элементам конструкций ЭМГ или к векторам переменных будет оговариваться в тексте.
Для пространственной векторной модели (рис. 1.6), так же как и для первичной модели (см. рис. 1.2), можно записать уравнения равновесия напряжение
Здесь, как и на рис. 1.6, u, i, W— пространственные векторы. Однако такг уравнения непосредственно нельзя решать совместно, поскольку переменные ст л\ тора записаны в статорной системе координат, а переменные ротора в роторной системе, т. е. вращаются относительно статора с угловой скоростью ю. В результате оси статора и ротор! сдвинуты относительно друг друга на переменный угол 6(t). Для того чтоб 1 привести уравнение роторной цепн к неподвижным осям статора, необходим^ вектор потокосцеплеиия ротора домножить на оператор поворота е~' , а зате' «заставить» все векторы уравнения ротора вращаться быстрее относительно ре-тора, увеличив их скорость на угловую скорость ротора, т.е. умножить члены уравнения ротора на оператор е [16]. Тогда получим
|
|
Бывает удобнее использовать при анализе не непосредственно векторные уравнения,
а уравнения в проекциях векторов на координатные оси [1, 10]. Обозначим эти оси dи q(рнс. 1.6), запишем систему (1.10) в проекциях на оси, как и на рис. 1.6, u, i, W— пространственные векторы. Однако такг уравнения непосредственно нельзя решать совместно, поскольку переменные ст л\ тора записаны в статорной системе координат, а переменные ротора (поме< >! ны верхним индексом г в скобках) в роторной системе, т. е. вращаются отно-j сительно статора с угловой скоростью ю. В результате оси статора и ротор! сдвинуты относительно друг друга на переменный угол 6(t). Для того чтоб 1 привести уравнение роторной цепн к неподвижным осям статора, необходим^ вектор потокосцеплеиия ротора домножить на оператор поворота е~' , а зате' «заставить» все векторы уравнения ротора вращаться быстрее относительно ре-тора, увеличив их скорость на угловую скорость ротора, т.е. умножить члены уравнения ротора на оператор е [16]. Тогда получим
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.