|
|
|
с начальным условием х(0) = Хц. В силу того что параметр 6 входит в уравнение линейно, его можно оценить по методу наименьших квадратов. Точностно эквивалентное управление, стабилизирующее систему, имеет вид и =- х - дх^. Обозначим через в = д-Q погрешность оценивания. Замкнутая система тогда приобретает следующий вид: |
|
|
|
hi Если оценка точна, последнее слагаемое исчезает и . экспоненциально сходится к нулю. Ситуация существенн иная при наличии ошибки оценивания. Предположим, что эт ошибка экспоненциально стремится к нулю, т.е. e(f) = ее Подставив последнее выражение в формулу (5), получи1 уравнение Риккати, имеющее решение |
|
|
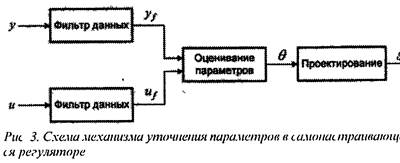
На ранних этапах исследования непрямых схем предполагалось, что объект представляет собой линейную динамическую систему, например систему с дискретным временем, описываемую уравнением
![]()
или эквивалентную ей с непрерывным временем. В силу того что неизвестные параметры входят в уравнение линейно, их можно оценить с помощью линейных регрессионных методов, например методом наименьших квадратов. К самонастраивающимся регуляторам применялось множество известных методов конструирования регуляторов, таких как расположение полюсов, LQG, * ff.
Интересное свойство самонастраивающихся регуляторов состоит в том, что их параметры могут сходиться к правильным значениям, даже если структура модели для их конструирования выбрана неверно. Это достаточно давно обнаруженное свойство исследовано в работах [32, 34, 35, 83]. В статье [90] показано, что самонастройка может не реализоваться для критериев качества типа обобщенных затрат; дальнейшие результаты по этой проблеме приведены в работе [52]. Анализ проблемы самонастройки дает понимание и вопросов сходимости параметров [18, 85, 1 14, 146].
2.4. Погрешности модели
Для непрямых схем естественно возникает несколько вопросов. Один из них - как быть с погрешностями оценивания. В проблеме оценивания присутствуют два типа погрешностей: смещение, объясняемое возможным неправильным выбором структуры модели, и погрешность, возникающая из-за случайных флуктуаций [91]. В первоначальных схемах конструирования регуляторов погрешности в оценках параметров игнорировались. Такое допущение называется "точностной эквивалентностью" (certainty equivalence) [126].
*LQG — зш)ача инмиттеского кчцструирониния регуляторы при линейных тршшчениях, кшдрититюм критерии кичестчи ч муссттй помехе. — Прим. пер.
Эта стратегия управления называется осторожным регулятором (cautious controller), поскольку она уменьшае7 отклонение и использует меньший коэффициент усиления при неточных оценках. Осторожное управление приближается к точностно эквивалентному при Р,/Ј' - 0.
Минимизация критерия (4) весьма затруднительна при п > > 1. Однако решения, которые можно определить численно, представляют несомненный интерес. Стратегии можно описать выражением
![]()
где/- функция, определяемая численно.
Эти стратегии близки к осторожному регулятору, когда оценки точны, т.е., когда отношение Р,1^ мало, а ошибка управления у, - у, велика. Они, однако, совершенно иные, когда величины Р,1^ и у, - у, малы. Управляющие сигналы, порождаемые данной стратегией, могут превосходить соответствующие сигналы при точностно эквивалентном управлении и осторожных регуляторах. Это объясняется тем, что закон управления генерирует управляющие сигналы, чтобы улучшить оценки. Причина, по которой в осторожном регуляторе не реализуются пробные воздействия, состоит в том, что временной горизонт составляет лишь один шаг, и стимул к пробным воздействиям отсутствует. О
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.