Другие предметы \ Приборы и системы управления

Настройка и адаптация. Адаптивное управление, страница 3

2.2 Прямые градиентные метод ы-адаптивные системы с эталонной моделью

Оптимизация была одной из первых попыток выработки механизма настройки параметров. Она привела к появлению адаптивного управления с эталонной моделью - одного из первых систематических подходов к адаптивному управле­нию. Применение этого подхода в управлении летательным аппаратом позволило создать адаптивную систему с эталон­ной моделью [143]. В основе этой системы лежат две идеи: 1) цель замкнутой системы формулируется как задача следования за моделью; 2) параметры регулятора настраиваются на основе градиентной схемы.

Рассмотрим, например, замкнутую систему с настраивае­мыми параметрами, типа изображенной на рис. 2. Идеальный отклик на входные сигналы определяется моделью, выход которой обозначим через у,„. Пусть у - выход объекта, а е = =у - ^„-ошибка. Введем функцию потерь J(e) = е^. Интуитив­но представляется разумным настраивать параметры так, чтобы функция потерь убывала. Это приводит к следующему закону настройки параметров

Этот закон называют "правилом М1Т". Величина де/дв в уравнении (1) - производная чувствительности [37]. С правилом М1Т связано несколько проблем. Одна из них состоит в том, что для построения производных чувствитель­ности часто требуются аппроксимации, что иллюстрируется следующим примером.

Пример 1

Рассмотрим простой контур с линейной обратной связью. Объект имеет передаточную функцию Р, а регулятор - С. Обозначим через R преобразование Далласа входного сигнала. Тогда преобразование Лапласа выходного сигнала замкнутой системы равно

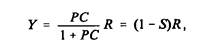
а преобразование Лапласа ошибки -

где Ь - нормально распределенная (со средним Ьц и дисперсией P(j случайная величина, с, - последовательность независимых нормально распределенных (с нулевым средним и единичной дисперсией) случайных величин.

Эта, на первый взгляд, простая задача весьма интересна. Проблема на самом деле достаточно сложна, поскольку знак параметра Ь неизвестен. Например, не существует стратегии робастного линейного управления, которая позволила бы стабилизировать систему.

Пусть допустимое управление таково, что и, - функция всех данных, имеющихся на момент 1, т.е. ^ = (^ ,, у/., k •= О, ..., [). Предположим, что требуется поддерживать выходную величину как можно ближе к величине у, в среднеквадратич­ном смысле. Это отражено в критерии


2.3. Непрямые схемы настройки -самонастраивающиеся регуляторы

Изображенная на рис. 2 схема настройки реализует прямой метод, поскольку значения параметров регулятора уточняют­ся непосредственно. При их косвенном уточнении - исходя из модели объекта - можно получить другую схему (рис. 3). Оцениваются параметры модели объекта, после чего парамет­ры регулятора находятся расчетным путем. Эту схему можно рассматривать как автоматизацию построения модели объекта и конструирования регулятора. Для получения хороших оценок можеттакже оказаться необходимым ввести возмуща­ющие сигналы с тем, чтобы убедиться, что объект возбужден. Эта функция в целях упрощения не показана на рис. 3. Оценивание параметров и конструирование регулятора можно провести множеством разных методом. Параметры можно уточнять на каждом такте или с меньшей скоростью.


Производная чувствительности в этом случае определя­ется выражением


где S = 1/(1 + PC) - функция чувствительности.

Для построения функции чувствительности необходимо, таким образом, знать функции чувствительности замкнутого контура. Это, в свою очередь, требует информации о неизвес­тном объекте. Следовательно, для вычисления функций чувствительности требуются аппроксимации.

Схема механизма настройки параметров приведена на рис. 2. Блок под названием "Эталонная модель" дает желаемый отклик на приложенные задающие сигналы, а производные чувствительности вырабатываются линейной динамической системой. Механизм настройки параметров нелинеен из-за умножения ошибки на производные чувствительности.

Правило М1Т весьма несложно. Его применение может привести, однако, к неустойчивым системам, в особенности если скорость адаптации высока.

Адаптивным системам с эталонной моделью были посвящены многочисленные исследования. Существует множество вариантов закона настройки, задаваемого уравнением (1). Весьма полезно нормализованное правило:
Скачать файл