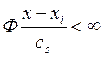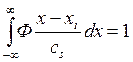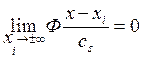Идентификация. Подстраиваемые модели. Методы структурной и параметрической идентификаций, страница 6

– ;

– ;

–;

Достоинства: можно быстро построить кривую регрессии y(x) при минимуме информации и требуется только статистика и качественная характеристика Ф. Можно использовать для сильно зашумленных объектов.

Недостатки: необходимость хранить обучающие выборки, которые занимают большой объем памяти. Возникают ситуации, когда разработка модели соизмерима со временем существования объекта управления.

Идентификация нелинейной динамической стохастической модели

Пусть дана выборка x(s) и y(s) статически независимых наблюдений, требуется установить неизвестную стохастическую зависимость. Алгоритм идентификации производится по формуле:

.

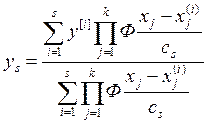Перед тем, как проводить идентификацию, необходимо произвести процесс генерации рабочей выборки из исходной обучающей. Применение рабочих выборок при построении непараметрических алгоритмов позволяет добиться двух положительных эффектов:

1. Уменьшить объем обучения выборки.

2. Уменьшить дисперсию оценки.

Непараметрические оценки позволяют решить следующие задачи:

1. Идентификация объектов (пассивными и активными методами).

2. Обучение распознаванию образов.

3. Проводить фильтрацию шума основного сигнала.

4. Оптимального и адаптивного управления и оптимизации процесса.

Идентификация объектов с внутренними связями

Рассматриваемые выше методы идентификации относятся к случаям, когда подстройка коэффициентов осуществляется для одного канала и каналов, влияющих друг на друга.

Рассмотрим случай, когда выход одного канала является входом  другого.

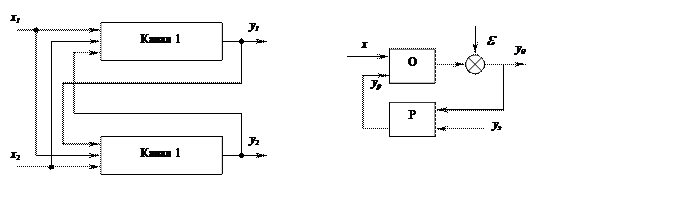В физическом смысле к числу характерных примеров такого рода относятся сталеплавильные процессы. Наиболее фундаментальным решением такого рода задач является вскрытие физических механизмов и динамическое описание этих взаимосвязей.

Эти объекты могут быть описаны следующей системой уравнений:

,

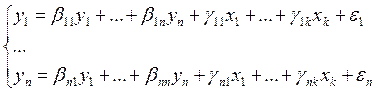где     k – количество независимых переменных;

          n – количество зависимых переменных.

Здесь возникает проблема неполной идентификации, т.к. число уравнений оказывается меньше числа оцениваемых параметров. Разработано несколько методов решения этих уравнений.

Метод наименьших квадратов

Система уравнений преобразуется к более простому виду:

,

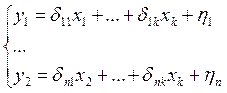где h – линейная функция ошибок. В нее входит все то, что не учли ранее. d и  h = f(b, g) – это нелинейная функция коэффициентов.

Эта система называется приведенной (сокращенной) формой.

Регрессии y₁, …, y_n на все x₁, …, x_k могут быть получены методом наименьших квадратов (если n = k). Если n ¹ k, то чтобы избежать этого затруднения, применяют априорные допущения, т.е. обнуляют некоторые коэффициенты, накладывают ограничения на другие коэффициенты. Рассмотрим реализацию представленного метода.

,    .

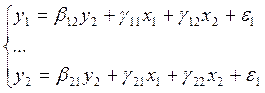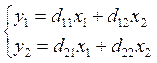Эта система решается методом наименьших квадратов. Учитываются ограничения и допущения и находятся коэффициенты d.

Разработка моделей имитаторов и тренажерных комплексов для повышения квалификации персонала

В связи с укрупнением металлургических агрегатов и повышению требований к качеству продукции требования к уровню квалификации персонала возрастают, чем выше сложность агрегата, чем  больше затраты. Для успешного решения задач повышения квалификации персонала необходимы новые методы и технические средства, к числу которых можно отнести тренажерные комплексы на основе математической модели, которые подтвердили свою эффективность в космической и авиационных сферах.

Тренажерные комплексы имеют достоинства:

1. Замена реального времени объекта научно информационной моделью, которая позволяет выделить некоторые стороны и редко встречающиеся аварийные ситуации.

2. Позволяет ввести поэтапную разработку с постепенным переходом от простого к сложному.

3. Возможность изменения параметров в пространстве и во времени.

4. Резкое сокращение материальных и экспериментальных затрат.

5. Возможность объективной оценки знаний и автоматизация процесса обучения.

6. Снижение психологической напряженности оператора.