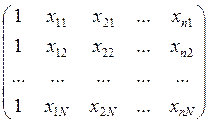Идентификация. Подстраиваемые модели. Методы структурной и параметрической идентификаций, страница 3

.

Это условие может быть нарушено, если ряд факторов x_ij в некоторых опытах окажутся стабилизированными, например, по условию технологии. Выходом из этой ситуации является увеличение числа опытов, либо второй выход – активное вмешательство в работу объекта. В противном случае приходится снижать число идентификационных параметров.

В качестве критерия идентификации чаще всего используется суммарная невязка (остаток) модели и объекта:

,

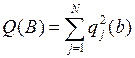где q_j – локальная невязка на j-м опыте:

.

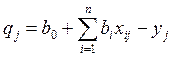Рассмотрим адаптивный шаговый метод. Суть метода: значение параметров модели связываются на двух следующих друг за другом шагах:

,

где J – алгоритм адаптации.

В качестве такого алгоритма часто используют метод наискорейшего спуска:

,

где q_j(B_j-1) – невязка на j-м шаге при значении параметра модели на (j – 1)-м шаге адаптации:

.

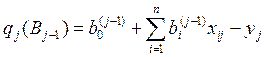Параметр a_j выбирается из условия минимума текущей невязки:

.

Достоинства метода: возможность использования текущей информации.

Недостаток: возникают проблемы сходимости процесса адаптации, они связаны с выбором параметра a_j.

Для непрерывного случая процесс адаптивной идентификации представляется дифференциальным уравнением вида:

.

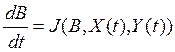Критерием идентификации здесь служит квадрат невязки, а алгоритмом – метод наискорейшего спуска, тогда уравнение:

,

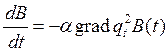где     B(t) = [b₀(t), b₁(t), …, b_n(t)];

          q_t(B) = b₀ + b₁x_1t + b₂x_2t + … + b_nx_nt – Y_t;

          .

Обозначив вектор X_t = [1, x_1t, x_2t, …, x_nt], получим:

q_t(B) = [B, X_t] – Y_t,

.

Уравнение адаптивной идентификации:

.

 

Параметрическая идентификация нелинейных моделей

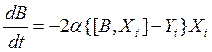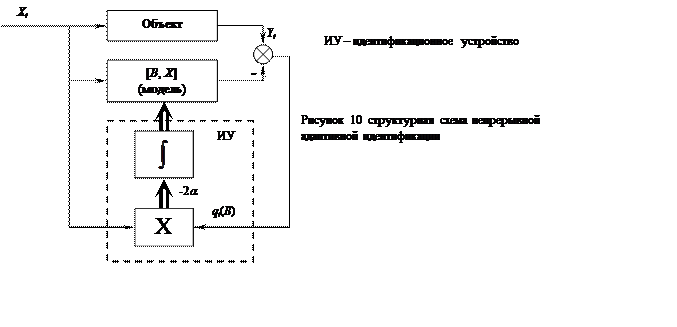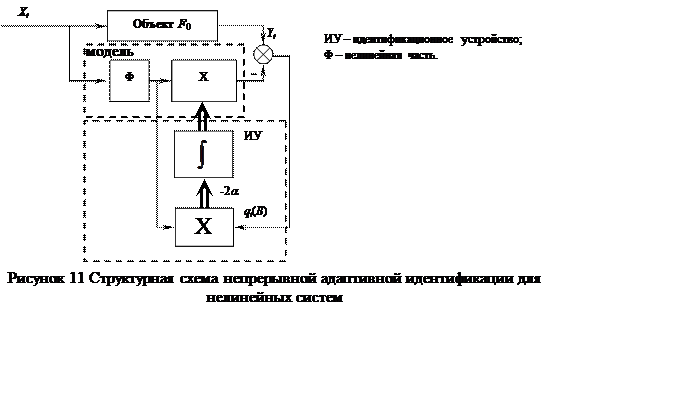
Структуру нелинейной модели предполагают в виде суммы линейных и нелинейных частей. В связи с этим алгоритм аналогичен линейному, только необходимо учесть нелинейность модели.

Объект отражается в виде функции F(X, B) с неизвестными параметрами B. Процедуры реализации функции основывается на кусочно-линейном или функциональном представлении в зависимости выхода модели от входа.

Неизвестная функция объекта F₀(X) представлена в виде известной функции с неизвестными параметрами Y = F(X, B). Чтобы определить неизвестные параметры B, приравнивают состояние модели и объекта для каждого из наблюдений:

F(X_j, B) = y_j, (j = 1..N),

где N ³ k, k – число оцениваемых параметров. Решение этой системы сводится к задаче минимизации суммарной невязки:

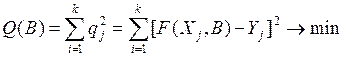
Рассмотрим особенности адаптивных методов идентификации применительно к непрерывным моделям. Для них локальная невязка:

.

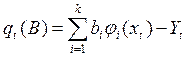Алгоритм проводится градиентным методом:

,

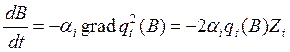где Z = (j₁(x₁), …, j_k(x_t)) – нелинейная часть модели.

Отличие от предыдущей схемы в том, что здесь присутствует функциональное преобразование Ф, которое предназначено для определения вектора Z_t.

Параметрическая идентификация стохастических объектов

Сначала рассмотрим случай статического стохастического объекта, его выражение Y = F₀(X, E), где E – вектор случайных факторов, порожденных либо самим объектом, либо средствами сбора и передачи информации. Рассмотрим случай, когда регулярная и случайная составляющая разделены, т.е.                   Y = F₀(X) + E.

Предполагается, что случайная составляющая E не зависит от входа X и оценивается плотность вероятности p[E]. Рассмотрим случай объекта с одним входом, т.е. m = 1. E обозначим за e. В этом случае плотность вероятности характеризуется двумя параметрами: математическим ожиданием и дисперсией:

m_e = M(e);   s² = M[(e – m_e)²].

Когда объект с двумя входами (m = 2). В этом случае случайная составляющая E = f(e₁,e₂). Плотность вероятности характеризуется для каждого входа: m₁=M(e₁); m₂=M(e₂); две дисперсии: s₁²=M[(e₁ – m_e)²] и s₂² = M[(e₂ – m_e)²], и корреляционный момент: K₁₂ = M[(e₁ – m₁)(e₂ – m₂)].