Идентификация. Подстраиваемые модели. Методы структурной и параметрической идентификаций, страница 4

Идентификация объектов с несколькими выходами значительно затрудняется, т.е. при наличии корреляционных помех, действующих на эти выходы. Преодолевается этот недостаток с помощью «декорреляции». Смысл ее заключается в следующем: пусть e₁ и e₂ коррелированные случайные величины, имеющие нулевые средние дисперсии  и  и корреляционным моментом K₁₂ (он известен), производим линейные преобразования и получаем новые случайные величины:

h₁ = a₁₁e₁ + a₁₂e₂; h₂ = a₂₁e₁ + a₂₂e₂.

Коэффициент корреляции:

.

Для того, чтобы корреляция была равна нулю, выполняется условие:

a₁₁ = 0;        .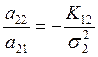

Таким образом можно избавиться от корреляционных помех на выходах (для каждого выхода).

В реальных условиях такая корреляция часто имеет место. Нужно получить значение корреляции . При известных значениях  может быть получены поправки Db₀, …, Db_n к значениям параметров b₀, …, b_n.

Чтобы определить параметр B после этапа структурной идентификации выбирается вид функции F, задача сводится к оптимизационной. Образуются невязки выхода модели и объекта на каждом j-м измерении:

q_j(B) = F(X, B) – y_j,        (j = 1, …, N).

Эта задача является многокритериальной и может быть решена только при свертывания критерия, что можно сделать, например, одним из способов:

– модульный критерий: ;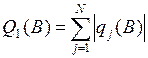

– квадратичный критерий: ;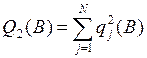

– показательный критерий: ;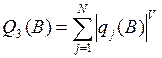

– минимальный критерий: ;

– взвешенный критерий: 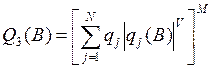, где q_j > 0.

Задача идентификации представляется в виде .

B^* – общий результат идентификации, этот результат зависит от типа критерия и вида модели. Выбор критерия зависит от характера помех. Например, при нормальном распределении помех наибольшую точность дает квадратичный критерий Q₂, который удовлетворяет требованиям простоты решения задачи ввиду гладкости функции вида Q(B).

Рассмотрим алгоритм пошаговой идентификации:

B_j = B_j-1 – 2a_j× q_j(B_j-1)Z_j.

Параметр a учитывает нелинейность модели и влияние вероятностной политики.

,

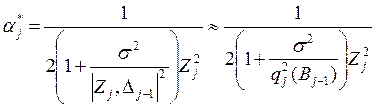где D_j-1 = B_j – B_j-1 – вектор невязки параметров.

Алгоритм адаптивной идентификации стохастического объекта имеет следующий вид:

.

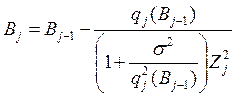Сходимость этого алгоритма зависит от Z_j. Нелинейная часть может увеличить сходимость процесса, но не гарантирует окончание идентификации за конечное число шагов из-за наличия помехи.

Идентификация динамических моделей

В идентификации различают параметрическую и непараметрическую модели объектов. Параметрические – это такие модели, которые определяются набором параметров, т.е. коэффициентов в процессе идентификации. Непараметрические модели определяются непрерывной функцией времени.

Линейная параметрическая модель для одномерного объекта представляется дифференциальным уравнением:

.

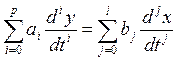Запишем модель в виде системы дифференциальных уравнений, т.е. делаем подстановку:

y₁ = y; y₂ = y⁽¹⁾; …; y_k = y^(k-1).

В результате получим:

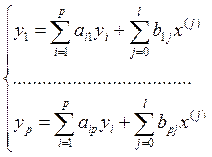 или .

Для многомерной линейной динамической системы уравнение будет:

.

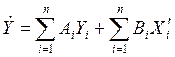Постановка задачи: определить такие  и , которые давали бы минимум критерию:

.

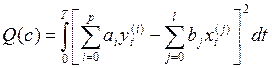Этот критерий должен стремиться к минимуму.

Оптимизация сводится к решению системы уравнений, образующейся, если приравнять нулю частные производные:

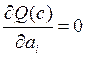, (i = 0..p – 1);  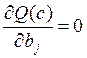, (j = 0..l).

После преобразования получаем систему алгебраических уравнений:

,

,       ,      .

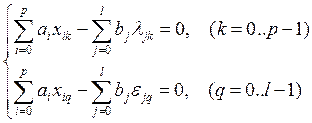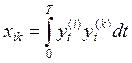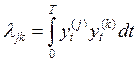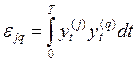Эта система является линейной динамической моделью.

Адаптивная идентификация динамических нелинейных моделей

Отличие: при обычной идентификации решение дифференциальных уравнений находится при заданных начальных условиях фиксируемых параметров.

Пусть F – известная функция F(y, x’, c). Здесь c – параметр, характеризующий линейную часть, y = y(t, c), c – фильтр.

При адаптивной идентификации невязка в момент времени c:

.

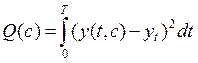Q(c) ® min. Минимизируется в каждый момент времени с (с₁,… , с_k).

Эта задача может быть решена с помощью поисковых методов оптимизации.