Идентификация. Подстраиваемые модели. Методы структурной и параметрической идентификаций, страница 5

D_x и D_y – операторы дифференцирования. Они способны усиливать помехи, особенно высокочастотные. Это приводит к необходимости применения устройств для сглаживания исходных сигналов Сг_x и Сг_y. Проблема сглаживания наиболее сложная. Основной задачей в этой проблеме является выбор такого оператора, который бы наилучшим образом подавлял помеху. Т.е. статические свойства помехи должны быть известны. Помеха должна в наименьшей степени искажать полученный сигнал.

Дискретный сглаживающий фильтр на основе экспоненциального сглаживания:

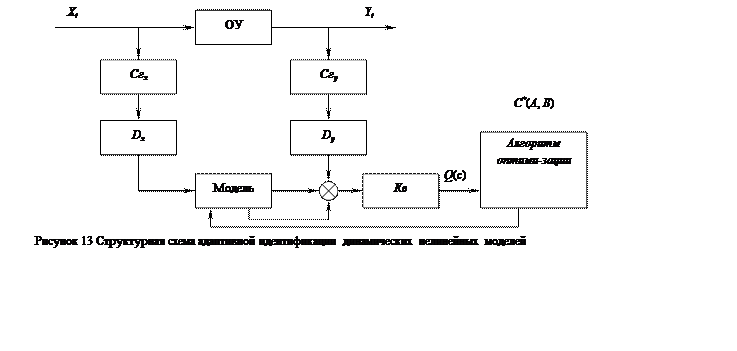
Оператор экспоненциального сглаживания: y_k+1 = ay_k + (1 – a)y_k-1,

где     y_k+1 – новое сглаженное значение;

          y_k-1 – предыдущее сглаженное значение;

          a – параметр сглаживания (0..1).

Если a = 1, то y_k+1 = y_k, тогда фильтр пропускает помехи, если a = 0,        y_k+1 = y_k-1, тогда фильтр поглощает все помехи.

Непараметрическая идентификация

Эта идентификация используется для модели, которая представляется в виде импульсной переходной характеристики, а также амплитудной и фазовой характеристиках.

Поведение объекта описывается интегралом свертки:

.

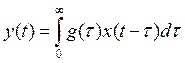Для стохастического случая, когда на вход объекта наряду с полезным сигналом действует помеха, то уравнение  статики-динамики принимает вид:

,

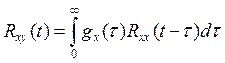где     R_xx – корреляционная функция входа;

          R_xy – антикорреляционная функция выхода.

Непараметрическую модель можно сделать параметрической:

.

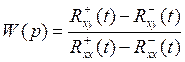Линейные динамические объекты описываемые непараметрической моделью, т.е. описываемые уравнением 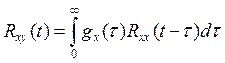 с целью идентификации переводят в параметрическую форму, а далее применяют процедуру идентификации линейной динамической модели.

Непараметрическая идентификация нелинейных динамических объектов

Модель Вольтера

В этой модели учитывается нелинейная часть динамического объекта. Моделью Вольтера называется ряд Вольтера:

.

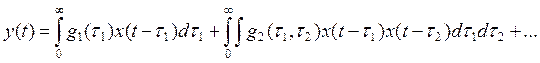Ряд Вольтера является функциональным обобщением ряда Тейлора. Его первый член отражает линейные динамические свойства объекта, второй – квадратичные свойства и т.д.

Идентификацию таких моделей производят следующим образом. Ряд представляют в дискретной форме, т.е. заменяют интеграл суммой:

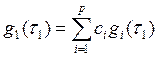 – линейная часть;  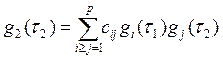  – нелинейная часть.

Подставляя данные выражения в ряд, получаем:

;

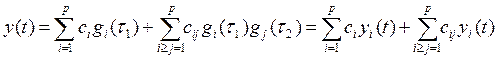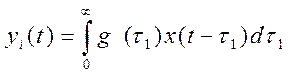, i = 1..p.

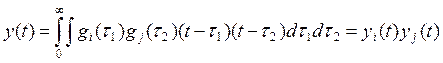, i ³ j = 1.

y_i – линейная часть;       y_j – нелинейная часть.

Задача идентификации сводится к следующему: найти параметры разложения данного ряда c = (c₁, …, c_p, c₁₁, …, c_pp), которые давали бы минимум критерию:

.

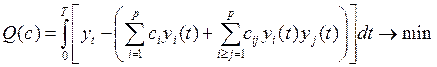Алгоритм решения выбирается в зависимости от конкретной ситуации. Если идентификация осуществляется в темпе с процессом или используется последовательное поступление информации, то в этом случае наиболее удобен алгоритм адаптивной идентификации.

В этом случае для определения коэффициента c можно использовать метод наискорейшего спуска, т.е.:

,    .

Модель Гаммерштейна

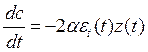Она основывается на том предположении, что нелинейность и динамику объекта можно разделить и представить в виде последовательного соединения двух звеньев: нелинейного (F_О1) и линейного динамического (F_О2): F_О =F_О1 ×F_О2. Таким образом здесь нужно идентифицировать две функции F_О1= f(×) и F_О2=g(t), определяющие выход модели:

.

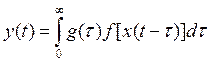Переход от непараметрической к параметрической идентификации осуществляется аналогично  модели Вольтера. Нелинейность модели устраняется введением новых параметров. После преобразования можно применить любой метод идентификации.

Непараметрическая идентификация динамических стохастических объектов

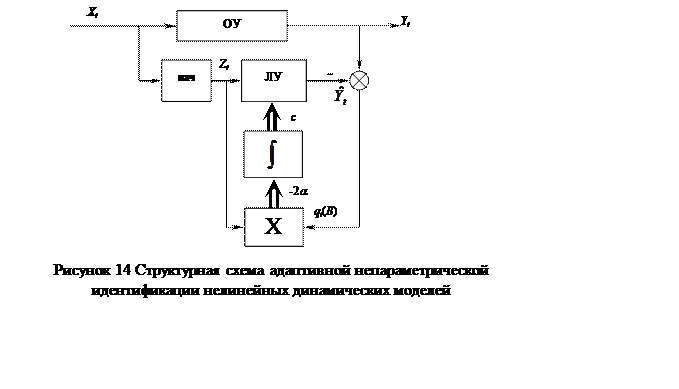
В последнее время для решения разнообразных задач кибернетики в условиях, когда размер априорной информации об исследовании процесса довольно мал и сведения о случайных факторах и других ограничениях не является исчерпывающим, возникает необходимость адаптивных систем, ориентированных на меньший объем информации, чем это требуется для математической постановки задачи.

В качестве оценки берется:

,

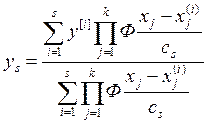где Ф – качественная характеристика объекта. Свойства этой характеристики: