Идентификация. Подстраиваемые модели. Методы структурной и параметрической идентификаций, страница 2

Вторая проблема параметрической идентификации смыкается с четвертым этапом.

В целом идентификация выступает как инструмент проверки гипотез о соответствии структуры или параметров объекта и модели на основе экспериментальных данных о его функционировании.

Содержательный анализ остатков как метод проверки гипотез об адекватности структуры

Под остатком (e_i) понимают разность между фактически измеренным y_i и предсказанным по модели  значениям выходного параметра. Остаток – это величина, которую не удается объяснить с помощью выбранной структуры модели, т.е. это остаточные ошибки модели. Относительно ошибок делаются следующие предположения: ошибки независимы, имеют нулевое среднее, постоянную дисперсию и подчиняются нормальному закону распределения. Если подбираемая модель находится в удовлетворительном соответствии с объектом, то остатки должны проявлять тенденцию к подтверждению выдвинутой гипотезе. После исследования остатков можно сделать два вывода (придти к одному из них):

1. Предположения по гипотезе нарушены.

2. Предположения по гипотезе не нарушены.

Процедуры исследования остатков

1. Общий вид (гистограмма распределения).

2. Зависимость от времени или номера опыта, если известны их последовательности.

3. Зависимость от предсказанных значений модели .

4. Зависимость от входных факторов x_ij.

5. Любой вид графика, который целесообразен для данной конкретной задачи.

1. Гистограмма распределения.

e =  – ошибка модели, n – число попаданий в интервал.

Если гистограмма имеет симметричный вид, то предположение модели верно.

Если несимметричный вид, то есть существует дополнительный локальный максимум, то это свидетельствует о том, что в модели не учтена неслучайная составляющая и требуется более глубокий анализ ошибки модели.

2. График временной последовательности. Возможно несколько характерных случаев.

На рисунке 9,а показана зависимость, при которой правильно выбрана структура модели и нецелесообразно ее дальнейшее совершенствование. Эффект времени не влияет на коридор ошибки. На рисунке 9,а дисперсия не постоянна, растет со временем (неправильно выбраны коэффициенты). На рисунке 9,в в модель не включен коэффициент, зависящий линейно от  времени. На рисунке 9,г в модели не учтены линейный и квадратный коэффициенты.

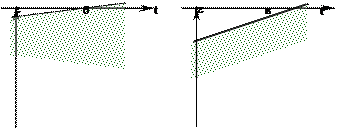
3. Зависимость от представленных значений модели . Графики аналогичны графикам на рисунке 9, но вместо времени t будет . Для (а) структура модели выбрана правильно, для (б) нужно использование метода взвешивания наименьших квадратов. Для (в) – допущена систематическая ошибка и пропущен свободный коэффициент.

Методы параметрической идентификации

Существует очень много методов идентификации. Разделим эти методы на зависимости свойств от модели:

1. Модели различают статические и динамические.

2. Детерминированные и стохастические.

3. Линейные и нелинейные.

4. Непрерывные и дискретные.

Идентификация делится:

1. Активные и пассивные методы.

2. Непрерывные и дискретные.

Параметрическая идентификация для статической детерминированной модели y = F(x)

Рассмотрим линейную модель объекта с n входами и m выходами, которая имеет единственно возможную структуру и описывается системой алгебраических уравнений:

.

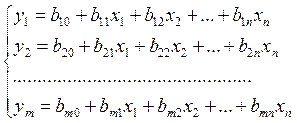В векторной форме эта система имеет вид Y = B₀ + BX.

Рассмотрим случай n > 1, m = 1, т.е. модель имеет один выход:

y = b₀ + [BX], или

y = b₀ + b₁x₁ + b₂x₂ + … + b_nx_n.

Модель содержит число k = n + 1 неизвестных параметров b₀, b₁,…, b_n, которые могут быть оценены на основе информации о работе объекта.

Рассмотрим неадаптивный шаговый метод применительно к решению этой задачи. Суть метода: приравниваются выходы объекта и модели в каждом из n опытов:

, .

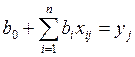В результате получается система из N уравнений идентификации с n+1 неизвестными, которая имеет однозначное решение, если ранг матрицы равен  n + 1, т.е. имеется n + 1 линейно независимых строк этой матрицы: