Стационарные задачи квантовой механики, страница 6

                   ,

т.е. превышает ту энергию, которой недостает частице, чтобы преодолеть барьер. Таким образом, есть вероятность приобретения  частицей энергии   и преодоления барьера. 

 Прохождение частиц сквозь потенциальный барьер доказывается анодной эмиссией электронов из металлов. Вырывание электронов из металлов электрическим полем происходит при напряженностях электрического поля в сотни раз меньших, чем те, которые необходимы для того, чтобы электрон в металле под действием внешнего электрического поля преодолел поверхностный скачок потенциала на границе металл-воздух и покинул металл. Действие электрического поля приводит к тому, что потенциальный барьер для электров на границе металл-воздух будет узким и электрон, обладающий энергией , сможет выйти из металла в результате туннельного эффекта. Есть и другие экспериментальные данные (-распад) подтверждающие туннельный эффект.

         Для широких барьеров и больших разностей (U -E) вероятность прохождения через барьер практически равна нулю, т.е. в этих случаях выводы квантовой теории совпадают с классическими. 

                          5.4.  Гармонический осциллятор

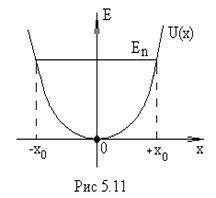          Гармоническим осциллятором называют частицу, совершающую одномерное движение под действием квазиупругой силы   . Потенциальная энергия такой частицы имеет вид:  (рис.5.11) . Собственная частота классического гармонического осциллятора  , где  m- масса частицы,   k - коэффициент упругости, тогда

                             .

Уравнение Шредингера для осциллятора:

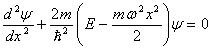,                 (5.8)

 где Е - полная энергия осциллятора.

    Это уравнение имеет конечные однозначные и непрерывные решения при значениях параметра Е

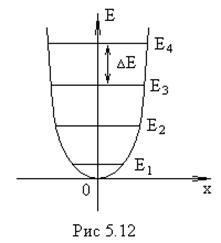
Схема энергетических уровней гармонического осциллятора представлена на рис.5.12.

 Уровни энергий вписаны в кривую потенциальной энергии и отстоят друг от друга на равные расстояния.

 Наименьшее возможное значение энергий равно . Это нулевая энергия.(т.е. та которой обладает частица при температуре абсолютного нуля ) Величина п, определяющая значения энергий (энергетические уровни) называется квантовым числом. Для гармонического осциллятора возможны лишь такие переходы квантовой системы из одного состояния в другое, при которых квантовое число п меняется на единицу .

             Условие, накладывемые   на изменение квантовых чисел, называется правилами отбора. Из правила отбора следует, что энергия гармонического осциллятора может меняться только  порциями  .

    Решение уравнения Шредингера для осциллятора будем искать в виде функции Гаусса . Возьмем вторую производную от этой функции и подставим в уравнение (5.8):

.

Подставив в уравнение (5.8), получаем

,

или  .