Стационарные задачи квантовой механики, страница 3

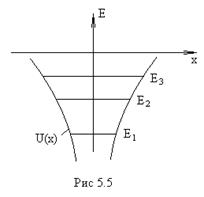
    Электрон, заключенный в ящике, является лишь очень грубой моделью атома водорода. Реальная яма является трехмерной, электрон в атоме находится в поле кулоновских сил, поэтому  стенки ямы имеют вид, представленный на рисунке 5.5. Однако поведение электрона в обеих ямах практически  одинаково и описывается стоячей волной, которой соответствуют собственные значения энергии 

Рассмотренная задача показывает, что движение квантовой частицы отличается от движения классической частицы тем, что:

1)  нельзя говорить о точном местонахождении частицы в яме, а можно говорить лишь о вероятности нахождения её в той или иной точке. Эта вероятность определяется величиной .

2)  Энергия квантовой частицы квантуется, т.е. принимает ряд дискретных значений ….

3)  Импульс квантовой частицы квантуется.

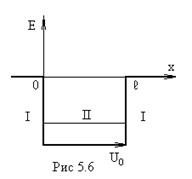5.2.Движение частицы в потенциальном ящике конечной  глубины

       Рассмотрим поведение частицы в потенциальном ящике конечной глубины. Потенциальная энергия частицы в ящике  при , вне ящика ( )  (рис.5.6).

        Примером такой ситуации является движение коллективизированных электронов внутри металла (согласно классической электронной теории вне металла потенциальная энергия электрона равна нулю, а внутри металла она отрицательна и равна ).

Применим к частице в таком потенциальном ящике уравнение Шредингера (будем считать, что задача одномерная, тогда )  .

 В области I       .  

  В области II         ,

или  

                  при                                                       

             при      

 (Е<0, т.к. потенциальная энергия отрицательна и превышает  кинетическую,   в противном случае частица выйдет из ящика). Нам нужно найти волновые функции  и энергии , которые бы удовлетворяли граничному условию такому, что   при  .

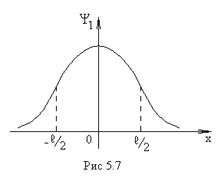
   Из классической теории следует, что  должна обращаться в ноль  при  т.к.   в этой области отрицательна, что соответствует отрицательным значениям кинетической энергии, запрещенным в классической физике, однако в этой области (I) уравнение Шредингера имеет решение:

где 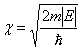, или    .                                                                                                                

В области II (при  ) решение уравнения Шредингера дает: ,  где , k имеет смысл волнового числа волны де Бройля. При     или    .