Стационарные задачи квантовой механики, страница 2

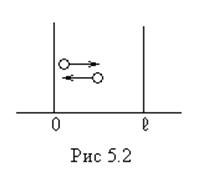
         Импульс частицы равен   , тогда согласно (5.3)  имеем:

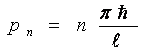
        - импульс частицы в ящике принимает  дискретные значения в соответствии с целым числом п, т.е. квантуется.

         Подставим (5.3) в (5.1) , имеем:

,  n=1,2…              (5.4)

- энергия частицы в ящике принимает ряд дискретных значений (квантуется).

        В теории колебаний доказывается, что уравнение Шредингера имеет решение не при любых значениях энергии, а лишь при избранных, которые называются собственными значениями энергии. Выражение (5.4) как раз и определяет эти значения. Каждой такой энергии отвечает стационарное состояние системы, т.е. такое, в котором распределение вероятностей обнаружить частицу не меняется. Решения, соответствующие собственным значениям , называются собственными функциями задачи. Наименьшее значение энергии достигается  при n=1:

                         .

Это энергия основного состояния. В квантовой механике частица не может иметь энергию, меньшую . С ростом n энергия растет. Вычислим расстояние между энергетическими уровнями:

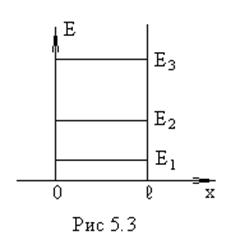     С ростом n расстояние между уровнями увеличивается (рис.5.3).

    Для молекулы газа в сосуде ,           энергетические уровни расположены так близко, что практически неразличимы, спектр можно считать сплошным.

  Для свободного электрона    и   эВ. Для электрона в атоме  ,        - дискретность уровней весьма заметна.

   Подставив k из (5.3)  в решение уравнения Шредингера (5.2), найдем собственные функции задачи:

Для определения  амплитуды а воспользуемся условием нормировки:

На концах промежутка интегрирования подынтегральная функция обращается в 0. Поэтому  значение интеграла получим, умножив среднее значение   на длину промежутка . Имеем:  тогда собственные функции:

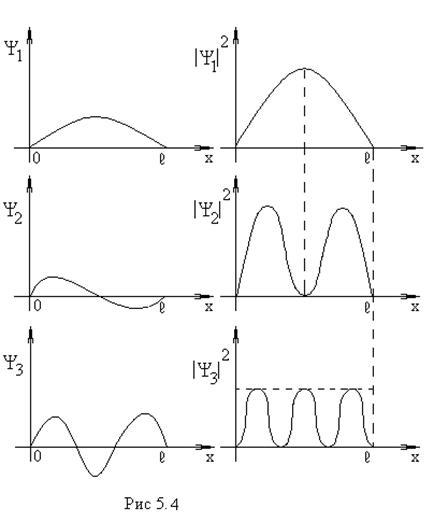На рисунке 5.4 показаны зависимости  и  для частицы при  n=1 и n=2. При n=1 вероятность обнаружить частицу в яме максимальная, а по краям ямы – равна нулю.    При   n=2 частица не может быть обнаружена в середине ямы, однако она одинаковое число раз бывает в левой и правой частях.