|
М |
етоды изученные в предыдущих параграфах позволяют решить любую схему. Но чем сложнее схема, тем с большим количеством преобразований придется столкнуться. К примеру, сначала схему необходимо будет свернуть до одного контура, найти необходимые значения, затем постепенно её разворачивать производя все новые и новые вычисления.
Это достаточно неудобно, и хотя закон Ома доказал свою универсальность, со временем стали появляться и другие более удобные методы. Основой для каждого из методов служит базисный закон – закон Георга Ома.
Густав Роберт Кирхгоф (1824-1887), профессор физики Гейдельберского университета в Берлине, в 1846 году установил два правила, названные в его честь[18] – «Первое и Второе правило Кирхгофа для электрических цепей»[19].
Первый закон Кирхгофа. Алгебраическая сумма токов в любом узле равна нулю.
При
выведении первого закона Кирхгоф опирался на закон сохранения
электрического заряда[20].
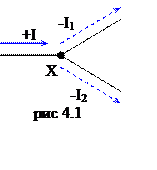
Если в разветвление X, проводящей цепи входит
ток силой I, а выходят токи I1
и I2, за время ∆t в область разветвления втекает электрический заряд ![]() , а вытекает заряд
, а вытекает заряд ![]() .
Приравнивая эти величины, друг к другу находим:
.
Приравнивая эти величины, друг к другу находим:
|
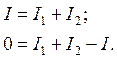
Если же в узле сходится n проводников, то
|
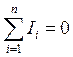
где под Ii понимают алгебраическую величину силы тока, которая берется со знаком «плюс», если ток входит в узел, и со знаком «минус» если выходит. Это правило называется правилом знаков.
Таким образом, мы получаем, что в один узел не могут втекать все токи из прилегающих ветвей, и из одного узла не могут вытекать все токи. Так как это нарушит закон сохранения заряда.
§ 4.2. Второй закон Кирхгофа для участка цепи.
 Как уже
говорилось, законы Кирхгофа включают в себя закон Ома. И второй закон для
участка цепи[21]
является прямым следствием закона Ома. Известно, что электрическое напряжение
есть разница электрических потенциалов между двумя точками. Тогда, пусть
электрические потенциалы в концевых точках участка цепи AB c сопротивлением
R есть
Как уже
говорилось, законы Кирхгофа включают в себя закон Ома. И второй закон для
участка цепи[21]
является прямым следствием закона Ома. Известно, что электрическое напряжение
есть разница электрических потенциалов между двумя точками. Тогда, пусть
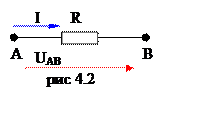
электрические потенциалы в концевых точках участка цепи AB c сопротивлением
R есть ![]() и
и ![]() рис
4.2. Тогда, по определению напряжения U на
участке АВ,
рис
4.2. Тогда, по определению напряжения U на
участке АВ,
|
а закон Ома приобретает вид:
|
Когда
на участке AB имеется
источник тока с ЭДС E, разность потенциалов
изменяется на величину ![]() , где знак выбирается в
зависимости от полярности включения источника (по току или против него).
Тогда соотношение 4.4 принимает вид:
, где знак выбирается в
зависимости от полярности включения источника (по току или против него).
Тогда соотношение 4.4 принимает вид:
|
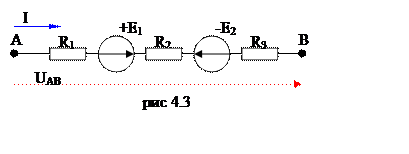 Если цепь сложная рис
4.3, то на пути от точки А к точке В может встретиться m источников тока ЭДС Ei и n сопротивлений Rk, по которым протекают токи Ik. Тогда второй закон Кирхгофа для участка цепи записывается
так:
Если цепь сложная рис
4.3, то на пути от точки А к точке В может встретиться m источников тока ЭДС Ei и n сопротивлений Rk, по которым протекают токи Ik. Тогда второй закон Кирхгофа для участка цепи записывается
так:
|
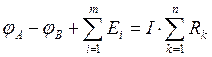
Из соотношения 4.6 выразим силу тока:
|
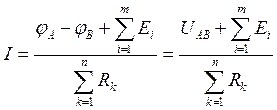
В такой записи это соотношение получило название обобщенный закон Ома. Для электрической схемы изображенной на рисунке 4.3 сила тока по обобщенному закону Ома будет выглядеть так:
|
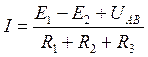
§ 4.3. Второй закон Кирхгофа для замкнутого контура.
Второй закон Кирхгофа для замкнутого контура. В любом контуре электрической цепи алгебраическая сумма ЭДС, источников напряжения, равна алгебраической сумме падений напряжения вдоль этого контура.
|
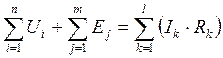
Второй закон Кирхгофа для замкнутого контура также основан на законе Ома и законе сохранения энергии – в замкнутой системе, сколько энергии излучается, столько же энергии и поглощается, таким образом, общее количество энергии остается неизменным.
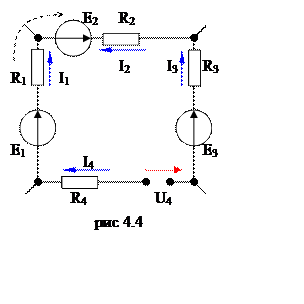 Возьмем, к
примеру, электрическую схему изображенную на рисунке 4.4. Стрелкой в
верхнем левом углу обозначен обход контура. Обычно, но не обязательно,
его направление выбирается по часовой стрелке. Обход необходим для правильного
составления уравнения, так как при записи уравнений по второму[22]
закону Кирхгофа используется следующее правило знаков:
Возьмем, к
примеру, электрическую схему изображенную на рисунке 4.4. Стрелкой в
верхнем левом углу обозначен обход контура. Обычно, но не обязательно,
его направление выбирается по часовой стрелке. Обход необходим для правильного
составления уравнения, так как при записи уравнений по второму[22]
закону Кирхгофа используется следующее правило знаков:
Если заданные или выбранные направления ЭДС, напряжений и токов в ветвях совпадают с обходом контура, то ЭДС в суммах слева, напряжения и токи в суммах справа записывают со знаком «плюс», если не совпадают с обходом контура – со знаком «минус».
Теперь составим уравнение для принципиальной электрической схемы, изображенной на рис 4.4. Направление токов выбрано совершенно случайно, только для этого примера.
|
§ 4.3. Метод решения задач на основе законов Кирхгофа.
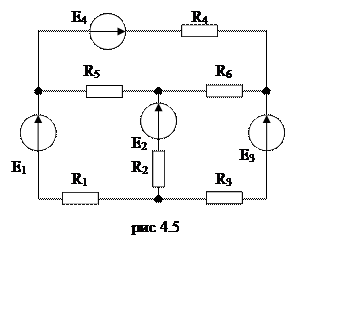 Для того чтобы уметь
применять законы Кирхгофа решим трех контурную электрическую цепь изображенную
на рис. 4.5.
Для того чтобы уметь
применять законы Кирхгофа решим трех контурную электрическую цепь изображенную
на рис. 4.5.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.