Решение задач по методу Кирхгофа, страница 5

Но можно было, и схитрить, применить первый закон Кирхгофа не только к узлам, но и к сечениям схемы. Это позволит не создавать новую систему уравнений 4.24.Нужно только переписать уже имеющуюся систему 4.21, с учетом того, что ветвь с сопротивлением R₅, а значит и током I₅, не существует.

	4.25		4.26

 

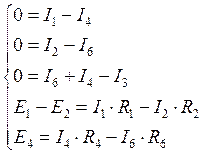
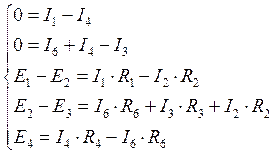Достаточно пяти уравнений, количество токов уменьшилось, и можно выкинуть любое уравнение. Поэтому системы уравнений 4.25 и 4.26 идентичны по результату.

Вывод: Если ток в ветви равен нулю, и в этой ветви нет активных[26] или реактивных[27] элементов, эту ветвь можно удалить из схемы без нарушения энергетической картины в ней.

§ 4.4. Построение диаграммы распределения электрического потенциала вдоль контура.

Для наглядного представления распределения электрического потенциала вдоль контура цепи и проверки правильности её расчета строят потенциальные диаграммы. Для любого контура цепи можно построить замкнутую потенциальную диаграмму: начав обход контура с выбранной точки, нужно придти к исходному потенциалу. График изменения потенциала, функции от сопротивления , вдоль контура служит графической иллюстрацией второго закона Кирхгофа.

Выбрав две любые точки в ветви, можно по направлению тока в ней, определить в какой из двух точек уровень потенциала будет выше. Ток течет по ветви, от точки с  большим потенциалом к точке с меньшим потенциалом. Если использовать понятия  из гидравлики, то предыдущее предложение будет звучать так: жидкость течет по трубе из точки с большим давлением к точке с меньшим давлением. Рассмотрим ветвь, в которой течет ток I₁. Ток течет от узла 4, через соединение 6, к узлу 1. Это означает, что в узле 4 уровень электрического потенциала максимальный, в соединении 6 уровень будет меньше, и в узле 1 он минимальный: . Таким образом, по уровню электрического потенциала в двух точках ветви, можно узнать направление электрического тока.

При составлении уравнений для  расчета значений электрического потенциала в точках контура используют следующие правила знаков.

Для ЭДС. Если ЭДС совпадает с направлением обхода контура, то значение ЭДС записываются со знаком «плюс», если не совпадает, записывают со знаком «минус». Или, если ЭДС[28] направленно от точки с меньшим потенциалом, к точке в которой уровень потенциала выше, значение ЭДС записывают со знаком «плюс», в противном случае, записывают со знаком «минус». Это происходит в силу того, что когда направление ЭДС совпадает с направлением тока в ветви, ЭДС как источник напряжения усиливает силу тока (по закону Ома, сила тока пропорциональна напряжению, и обратно пропорциональна сопротивлению), тем самым, повышая уровень потенциала для точки находящейся за ЭДС по направлению тока в ветви. В обратном случае, когда направление тока и ЭДС не совпадает, ЭДС препятствует движению тока в ветви, ослабляя его, соответственно уровень электрического потенциала для данной точки будет ниже.

Для сопротивлений. Когда направление тока в ветви совпадет с направлением обхода контура, значения для всех падений напряжений записываются со знаком «минус», в противном случае – со знаком «плюс». Или, если в первой точке ветви, по обходу контура, уровень электрического потенциала больше чем во второй, то значения для всех падений напряжений записываются со знаком «минус», в противном случае – со знаком «плюс». Это правило знаков объясняется тем, что на сопротивлении всегда происходит падение напряжения.

 

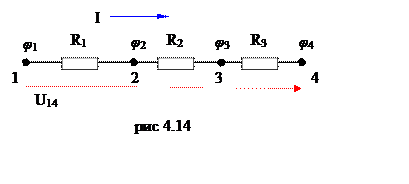Для ветви изображенной на рис 4.14 сила тока будет равна 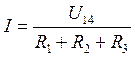. Напряжение на каждом из резисторов будет равно: , , . Теперь, если принять за начало системы отсчета точку 1, и направление по току, то общее напряжение будет равно максимальному потенциалу в точке 1, минус потенциал в точке 2, 3, и в точке 4. . Переходя от точки к точке мы теряем напряжение. Эсли предположить, что ветвь замкнута концами 1 и 4 на себя, и между ними существует источник напряжения Е, то потенциал точки 1 будет равен , а для точки 4 будет равен .