· 1: токи I1, I5, I2;
· 2:токи I6, I3, I2;
· 3:токи I4, I5, I6;
· 4: токи I1, I4, I3 – внешний контур;
· 5: токи I1, I5, I6, I3.
 В этой схеме,
чтобы учесть все токи, сопротивления, и источники ЭДС достаточно составить
уравнения для любых трех контуров. А как быть, если нужно рассчитать сложную
схему? Искать все контура и составлять для каждого свое уравнение, чтобы потом
выбрать нужные? Есть более простой способ. Нужно составить уравнения только для
линейно независимых контуров. Необходимо выбрать контуры таким образом,
чтобы в каждый из них входило не меньше одной ветви, не вошедшей в предыдущие
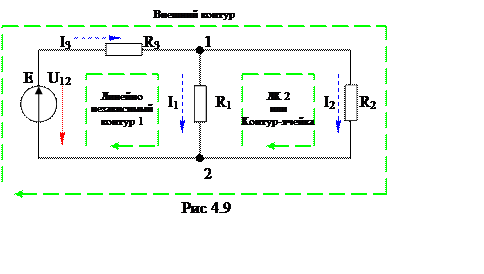
контуры. При этом условии полученные уравнения будут независимые. На рис 4.9
изображена схема из двух линейно независимых, и одного внешнего контура.
В этой схеме,
чтобы учесть все токи, сопротивления, и источники ЭДС достаточно составить
уравнения для любых трех контуров. А как быть, если нужно рассчитать сложную
схему? Искать все контура и составлять для каждого свое уравнение, чтобы потом
выбрать нужные? Есть более простой способ. Нужно составить уравнения только для
линейно независимых контуров. Необходимо выбрать контуры таким образом,
чтобы в каждый из них входило не меньше одной ветви, не вошедшей в предыдущие
контуры. При этом условии полученные уравнения будут независимые. На рис 4.9
изображена схема из двух линейно независимых, и одного внешнего контура.
Из вышесказанного следует, что минимальное количество линейно независимых контуров в схеме будет равно двум. Вспомним топологические определения для ветви, узла и контура.
Ветвь – участок электрической цепи, по которой протекает один и тот же ток.
Узел – место соединения трех и более ветвей электрической цепи. Место соединения двух ветвей называют соединением.
Контур – замкнутый участок цепи.
от сюда: на одну ветвь всегда приходиться два узла. Из 1ЗК следует, что достаточно У-1 узлов для описания всех токов в ветвях. Число линейно независимых контуров связано с числом ветвей В, и числом узлов У в цепи. Таким образом необходимо: от количества ветвей в схеме вычесть количество узлов, и вычесть единицу, поскольку один узел можно не учитывать по 1ЗК.
|
Количество узлов для задачи уже известно: У=4, а количество ветвей равно шести. Из формулы 4.16 следует, что на основе второго закона Кирхгофа необходимо составить N2ЗК уравнений:
|
Запишем, и разберем их.
|
|
|
Разберем
формулу 4.18. Второй закон Кирхгофа для замкнутого контура звучит так: в
любом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической
сумме падений напряжения вдоль этого контура. Перейдем к ЭДС в левой части
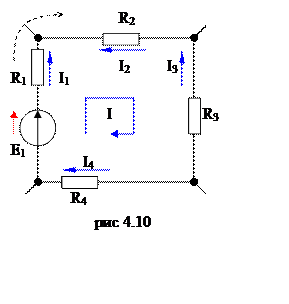
уравнения. Направление обхода для контура в нашей схеме совпадает с
движением по ходу часовой стрелки (смотри рис 4.6). Если направление[24]
ЭДС, для этого контура, совпадает с направлением обхода, то ЭДС берется со
знаком «плюс», если не совпадает – со знаком «минус». Е1
совпадает с направлением обхода[25],
Е2 - не совпадает. Отсюда в левой части уравнения записываем ![]() .
.
Если в контуре нет ЭДС или другого источника напряжения, тогда в левой части уравнения нужно записать число «ноль»
 В правой части
уравнения записываем алгебраическую сумму падений напряжений. Формула 4.9 математически
описывающая второй закон Кирхгофа является, вариантом закона Ома
В правой части
уравнения записываем алгебраическую сумму падений напряжений. Формула 4.9 математически
описывающая второй закон Кирхгофа является, вариантом закона Ома ![]() . Закон Ома описывает участок электрической
цепи - ветвь, с одним сопротивлением, и с одним источником напряжения ЭДС. А
теперь, представьте, что концы ветви замыкаются друг на друга, получаем
замкнутый контур. В этом случае закон Ома не теряет своей справедливости.
. Закон Ома описывает участок электрической
цепи - ветвь, с одним сопротивлением, и с одним источником напряжения ЭДС. А
теперь, представьте, что концы ветви замыкаются друг на друга, получаем
замкнутый контур. В этом случае закон Ома не теряет своей справедливости.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.