Теперь,
если в выбранную ветвь добавить несколько сопротивлений ![]() то
получим, что через каждое сопротивление течет один и тот же ток I. Это можно наблюдать на схеме рисунка 4.10. Но
это верно только в тех случаях, когда у нас всего один контур, или мы намеренно
забываем, что исследуемый контур связан своими ветвями с другими, соседними,
контурами. А раз каждая ветвь является смежной, то мы не можем гарантировать,
что ток в ней не будет завесить от источников напряжения и сопротивлений в соседнем
контуре. Поэтому для каждой ветви отдельно расписывается, на сколько вольт в ней
падает напряжение. Направление тока в ветви влияет на знак в алгебраической
сумме, если направление условно положительного тока для данного контура
совпадает с направлением обхода, слагаемое суммы берется со знаком «плюс»,
если не совпадает – со знаком «минус».
то
получим, что через каждое сопротивление течет один и тот же ток I. Это можно наблюдать на схеме рисунка 4.10. Но
это верно только в тех случаях, когда у нас всего один контур, или мы намеренно
забываем, что исследуемый контур связан своими ветвями с другими, соседними,
контурами. А раз каждая ветвь является смежной, то мы не можем гарантировать,
что ток в ней не будет завесить от источников напряжения и сопротивлений в соседнем
контуре. Поэтому для каждой ветви отдельно расписывается, на сколько вольт в ней
падает напряжение. Направление тока в ветви влияет на знак в алгебраической
сумме, если направление условно положительного тока для данного контура
совпадает с направлением обхода, слагаемое суммы берется со знаком «плюс»,
если не совпадает – со знаком «минус».
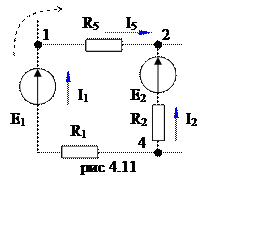 Для выбранного
контура (рис 4.11), направление токов I1
и I5 совпадает с направлением обхода
в контуре, поэтому записываем падение напряжения на сопротивлениях R1 и R5 со
знаком «плюс»
Для выбранного
контура (рис 4.11), направление токов I1
и I5 совпадает с направлением обхода
в контуре, поэтому записываем падение напряжения на сопротивлениях R1 и R5 со
знаком «плюс» ![]() . Направление тока I2 не совпадает направлением обхода –
записываем со знаком «минус»
. Направление тока I2 не совпадает направлением обхода –
записываем со знаком «минус» ![]() .
.
Аналогично расписываем уравнения для всех оставшихся контуров.
В результате получаем три уравнения, написанные по первому правилу Кирхгофа и три по второму. Теперь можно создать систему из шести уравнений.
|
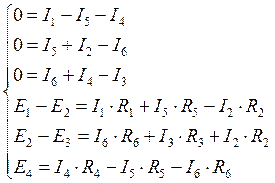
Решением этой
системы уравнений будет: 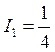 ,
, 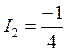 ,
, ![]() ,
, 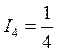 ,
, ![]() ,
, 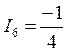
Решив систему 4.21, мы нашли условно положительные токи, и теперь необходимо превратить их в реальные токи.
 Реальные токи
отличаются от условно положительных токов своим направлением. Переход к
реальным токам очень прост. Если условно положительный ток больше или равен нулю,
то направление реального тока совпадает с направлением условно положительного
тока. Если условно положительный ток меньше нуля, то направление реального тока
противоположно направлению условно положительного тока.
Реальные токи
отличаются от условно положительных токов своим направлением. Переход к
реальным токам очень прост. Если условно положительный ток больше или равен нулю,
то направление реального тока совпадает с направлением условно положительного
тока. Если условно положительный ток меньше нуля, то направление реального тока
противоположно направлению условно положительного тока.
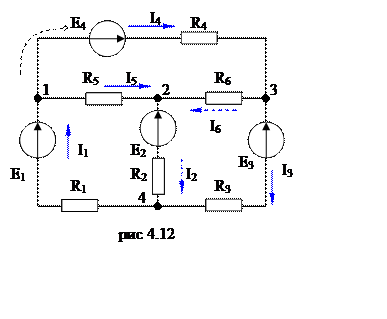
Для нашей задачи, условно положительное токи изображенные на рис 4.6, примут направление, отображенное на рис 4.12. Токи, которые изменили, свое направление это I2 и I6 прорисованы пунктирными линиями.
Теперь
после того как мы нашли значение токов и их направление можно переходить к
расчету баланса мощностей. Напомню главное правило при расчете – баланс
мощностей должен сходиться ![]() . Если баланс не
сходиться, Вы ошиблись или в расчетах, или в направлениях токов, или запутались
в ветвях.
. Если баланс не
сходиться, Вы ошиблись или в расчетах, или в направлениях токов, или запутались
в ветвях.
|
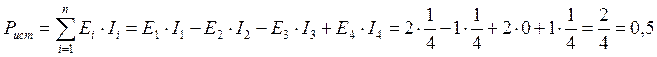 ватт
ватт
|
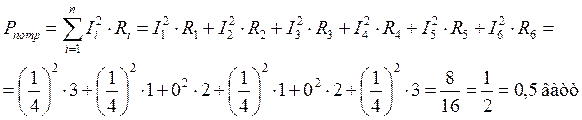
 Обратите внимание,
что токи I3 и I5
равны нулю. Это значит, что ток через ветви с сопротивлениями R3
и R5 не течет. Поэтому можно использовать
резисторы с любым значением сопротивления, от нуля до «бесконечности». Но это
не значит, что эти ветви можно удалить или разорвать их. К примеру, ветвь, в
которой протекает ток I3 нельзя
разрывать, так как в ней находиться источник напряжения ЭДС, благодаря которому
поддерживается установленный уровень напряжения во всей цепи. Если разорвать
эту ветвь, измениться вся энергетическая картина в цепи.
Обратите внимание,
что токи I3 и I5
равны нулю. Это значит, что ток через ветви с сопротивлениями R3
и R5 не течет. Поэтому можно использовать
резисторы с любым значением сопротивления, от нуля до «бесконечности». Но это
не значит, что эти ветви можно удалить или разорвать их. К примеру, ветвь, в
которой протекает ток I3 нельзя
разрывать, так как в ней находиться источник напряжения ЭДС, благодаря которому
поддерживается установленный уровень напряжения во всей цепи. Если разорвать
эту ветвь, измениться вся энергетическая картина в цепи.
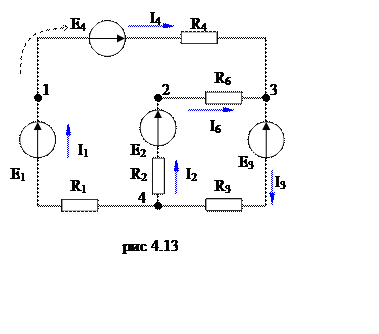
А вот ветвь, в которой протекает ток I5, можно спокойно убрать из схемы (см. рис. 4.13), в ней нет активных или реактивных элементов. Доказательством этого будет решение системы уравнений:
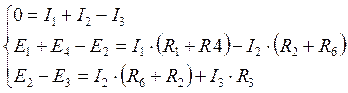
|
Решением этой
системы будут токи: 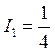 ,
, 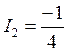 ,
, ![]() . Откуда по закону Ома находим токи:
. Откуда по закону Ома находим токи: ![]() ,
, ![]() . Так
что токи, найденные через решение системы уравнений 4.24 совпадают, с
токами, найденными через систему уравнений 4.21.
. Так
что токи, найденные через решение системы уравнений 4.24 совпадают, с
токами, найденными через систему уравнений 4.21.
Создавая систему уравнений 4.24, мы пошли по прямому пути, применили первый закон Кирхгофа к узлам схемы, в схеме после преобразования осталось два узла (3, 4) и два сечения (1, 2). И воспользовались следствием закона Ома, сложив сопротивления R1 c R4 и R2 c R6 помня что: ток, протекающий по ветви, будет один и тот же для каждого элемента этой ветви – сопротивлений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.