Решение задач по методу Кирхгофа, страница 2

Задача: Даны сопротивления и ЭДС, необходимо найти силы токов для каждой из ветвей, рассчитать баланс мощностей и построить диаграмму распределения электрического потенциала.

Дано:

·  R₁= R₆=3 Ом, R₂= R₄ =1 Ом, R₃= R₅=2 Ом;

·  E₁= E₃=2 В, E₂=E₄=1 В.

Для начала необходимо выбрать направление обхода контура. Пусть в нашем случае направление обхода контура  будет по ходу часовой стрелки. Затем присвоим каждому узлу номер. Эта визуализация позволит не наделать ошибок.

После этого нужно выбрать условно положительное направление электрического тока в ветвях. Для этого существует ряд простых правил:

·  Направление тока одинаково для всех элементов одной ветви;

·  Направление силы тока в ветви обычно выбирают по направлению ЭДС, если ЭДС в ветви отсутствует, то следуют первому закону Кирхгофа;

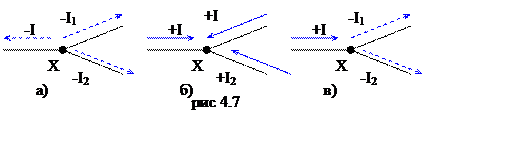
·  Следуя первому закону Кирхгофа, выбираем направление тока в ветви так, чтобы алгебраическая сумма токов в прилегающих узлах была равно нулю. Так, чтобы в узел втекал и вытекал хотя бы один ток из прилегающих ветвей. На рисунке 4.7 показаны: не правильные варианты а) и б), и правильный в).

· 

Чтобы не запутаться в дальнейших расчетах, по возможности индексы токов в ветвях должны совпадать с индексами элементов, по которым эти токи протекают.

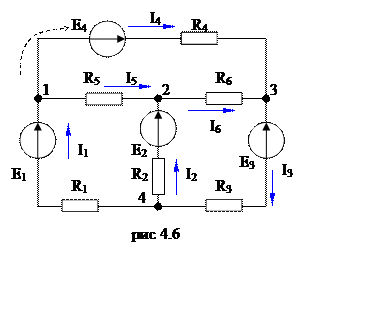
После нанесения условно положительных токов и направления обхода схема примет вид, показанный на рис 4.6.

Следующим шагом будет создание системы уравнений на основе первого и второго законов Кирхгофа.

Первый закон Кирхгофа применим к узлам цепи. В схеме на рис 4.6 4 узла. Чтобы описать все токи, втекающие и вытекающие в эти узлы, достаточно 3-х уравнений. С помощью уравнений по 1ЗК мы описываем все токи в узле из смежных (прилегающих) ветвей. Токи в смежных ветвях, в свою очередь, пересекаются в других узлах, дополняя друг друга. Или: ток, протекающий по одной ветви, втекает в один узел и вытекает из другого узла. Для узла B на рисунке 4.8 ток I₁ втекает, а для узла A – вытекает.

Таким образом, для описания любой электрической схемы, достаточно всего N уравнений 1ЗК = количество всех Узлов схемы минус 1.

4.11

4.12

Для нашей задачи . Теперь запишем уравнения.

·  Для первого узла: ;

· 

4.13

Для второго узла ;

· 

4.14

Для третьего узла .

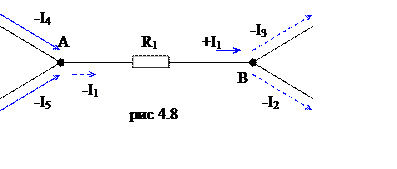
Чтобы не осталось недопонимания, разберем уравнение 4.12. Как следует из первого закона Кирхгофа, алгебраическая[23] сумма токов в любом узле равна нулю. Раз так, в левой части уравнения смело ставим ноль. Для правой части уравнения, токи втекающие в узел записываются со знаком «плюс», вытекающие из узла – со знаком «минус». Ток I₁ втекает в узел, токи I₅ и I₄ вытекают из узла. Поэтому, в правую часть уравнения заносим . Точно также поступаем и для других узлов.

Еще раз напоминаю, что можно было взять любые три узла, это могли быть и 1, 3, 4, или 2, 3, 4. Их будет достаточно для описания схемы. А уравнение для четвертого узла будет выглядеть следующим образом:

4.15

Для решения задачи с шестью неизвестными необходимо составить шесть уравнений. У нас пока есть только три уравнения. Остальные составляются на основе второго закона Кирхгофа для замкнутого контура.

Когда мы составляли уравнения для узлов, на основе первого закона Кирхгофа, мы столкнулись с тем, что достаточно N уравнений. Где N равно количество узлов минус единица. В случае составления уравнений для контуров, на основе второго закона Кирхгофа, наблюдается похожая ситуация. Для составления соотношений между падением напряжения и напряжением в контуре требуется меньшее количество уравнений, чем существует контуров в схеме.

В нашей задаче пять контуров: