Эквивалентные преобразования – эквивалентный треугольник, эквивалентная звезда

Эквивалентные преобразования – эквивалентный треугольник, эквивалентная звезда.

В электрических цепях наряду с последовательным и параллельным соединением часто встречается  соединения элементов, называемые треугольником и звездой.

Треугольником называют соединения трех элементов,  в котором конец первого элемента соединен с началом второго, конец второго с началом третьего,  конец третьего с началом первого.

Звездой называют соединение, в котором концы трех элементов соединены  в одну общую точку n.

Если произвести эквивалентную замену треугольника на звезду, то число узоров в схеме уменьшиться и расчет цепи упроститься. Эквивалентность такой замены проявляется в том, что токи I₁, I₂, I₃ в ветвях, примыкающих и к треугольнику и к звезде, и напряжения между узлами 1, 2, 3 остаются одними и теми же, или изменяются одинаково для всех режимов работы обоих схем, в том числе при обрыве одного из проводов, подходящих, например, к узлу 1. При этом изменившийся ток I₂ треугольника  должен быть равен I₂ звезды, а ток I₃ звезды – равен току I₃ треугольника, что возможно только при равенстве сопротивлений между узлами 2 и 3 треугольника и звезды (аналогично при обрыве проводов, подходящим к узлам 2 или 3):

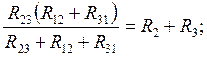
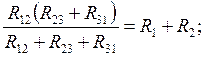
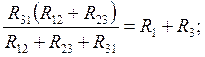
Решив систему, например, вычтя из второго уравнения первого и сложив результат с третьим уравнением и т.д., получим:

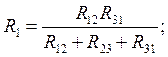
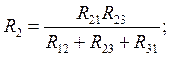
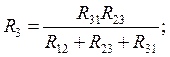
т.е. сопротивление луча эквивалентной звезды равно дроби, в числители которой произведение двух сопротивлений треугольника, примыкающих к искомому узлу, а в знаменателе – сумма всех сопротивлений треугольника.

Обратное преобразование звезды в эквивалентный треугольник получим (деля,  например, первое уравнение на второе, первое на третье уравнение и т.д. и решая их совместно)

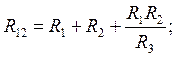
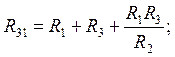
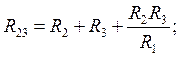
т.е. сопротивление ветви треугольника равно сумме сопротивлений резисторов звезды, примыкающих  к соответствующим узлам, плюс произведение этих резисторов, деленное на сопротивление третьего резистора звезды.

Если  R₁ = R₂ = R₃ = R_Y, то сопротивление каждой ветви треугольника R_D = 3R_Y, а при R₁₂ = R₂₃ = R₃₁ = R_D, сопротивление каждого луча звезды