










Глава 3. Методы совершенствования гирокомпасов двухгироскопнного класса.
В этой главе отчета исследуется один из возможных вариантов построения на базе чувствительного элемента гирокомпасов класса
" Standard" или "Курс" корректируемого гирогоризонткомпаса.
Точность корректируемого гирогоризонткомпаса (КГГК) будет более высокой по сравнению с современными двухроторными гирокомпасами при маневрировании и в условиях качки судна. Помимо этого, КГГК будет выдавать информацию о крене и дифференте судна, знание которой необходимо для автоматической настройки систем автоматического управления движение судна по заданному курсу, что, в конечном счете, приводит к уменьшению потери скорости судна.
Точность визуального съема информации о курсе, крене или дифференте в КГГК выше, так, как в КГГК нет кардановой погрешности. Для повышения точности взятия пеленгов и определения курсовых углов пеленгаторные репитеры стабилизируются относительно плоскости горизонта при качке судна
Все изложенное показывает, что такой прибор, в котором используются уже выпускаемые отечественной промышленностью чувствительные элементы, может быть создан с меньшими затратами и в более короткие сроки. Поэтому исследование этой проблемы вполне актуально.
3.1. Классификация корректируемых ГГК.
Теория КГГК имеет особенность, отличающую ее от теории двухгироскопных гирокомпасов тем, что следящая сфера ГК стабилизируется по отношению к гиросфере по одной координате для автоматического съема информации о непрерывно изменяющемся, при движении судна, курсе К(t). Эта сфера в КГГК стабилизируется по отношению к гиросфере по крайней мере по двум координатам и теперь она является стабилизированным по отношению к гиросфере элементом.
Благодаря этому новому качеству стабилизированную сферу (сокращенно "стабсферу") теперь используют, как платформу.
Чтобы управление было корректным точка подвеса гиросферы и стабсферы должны совпадать. Поэтому центрирование гиросферы относительно стабсферы производится с помощью металлических торсионов. С помощью этих же торсионов на гиросферу КГГК налагаются как управляющие, так и корректирующие моменты.
По способу реализации подвеса гиросферы внутри стафбсферы КГГК подразделяются на две модели. В первой модели КГГК гиросферы подвешиваются с помощью одной пары горизонтальных торсионов. Этот способ гораздо проще и его легче реализовать. В дальнейшем эти КГГК будут иметь обозначение КГГК-1.
Во второй модели КГГК-2 применяется двухосный торсионный подвес в виде двух пар торсионов, одной горизонтальной, другой вертикальной.
Во всех моделях КГГК центр тяжести гиросферы совмещен с точкой ее подвеса. Для придания гиросфере свойства избирательности по отношению к плоскостям меридиана, и горизонта в КГГК реализуется косвенный способ управления ее движением. Датчиками управляющих сигналов в этом способе управления являются акселерометры AN-W и AE-W, установленные в гиросфере.
Положение статического равновесия КГГК-2 при движении судна постоянными скоростью и курсом находится в плоскости истинного горизонта и истинного меридиана, а у КГГК-1 в плоскости истинного горизонта и плоскости гирокомпасного меридиана, положение которого определяется скоростной девиацией.
3.2 Уравнения движения корректируемого ГГК
Для получения уравнений движения гироскопического чувствительного элемента КГГК воспользуемся уравнениями движения двухроторной гиросферы полученными Я.Н. Ройтенбергом
и имеющими следующий вид (4):
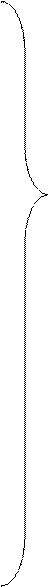
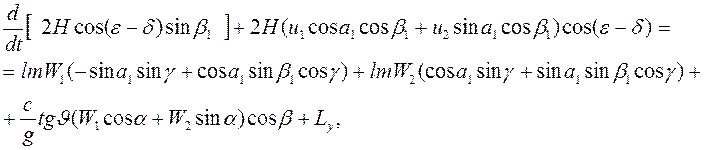
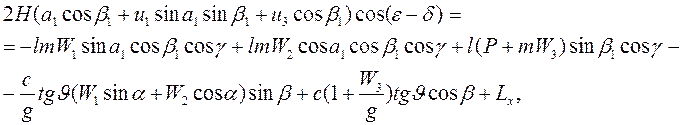 (3.1)
(3.1)
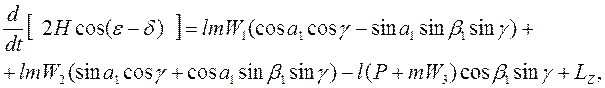
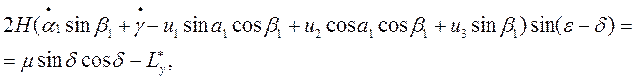
![]()
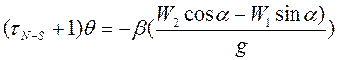 .
.
В этой системе уравнений использованы обозначения:
α1 , β1 , γ - углы Эйлера, которым определяется углы поворота координатных осей x, y, z гиросферы относительно географической координатной системы ξ ζ η. Оси этой системы направлены так: ось η- на север, ось ξ - на восток, а ось ζ по радиусу Земли вверх.
θ-угол, определяющий избыток жидкости в сосудах по сравнению с их средним положением,
ε- угол, определяющий начальные положения главных осей гироскопов относительно главной оси Z гиросферы,
δ- угол, определяющий величину отклонения главных осей
z1 и z2 гироскопов от их начального положения ε= 45º по отношению к главной оси гиросферы,
![]() -постоянная времени гидравлического демпфера,
-постоянная времени гидравлического демпфера,
![]() - кинетический момент гироскопа,
- кинетический момент гироскопа,
m- масса гиросферы,
Ky - коэффициент пропорциональности, характеризующий упругость пружин спарника,
ω- угловая скорость вращения Земли,
φ- широта места,
V- скорость судна.
Проекции мгновенной угловой скорости гиросферы на оси ξ ζ η равны:
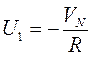 ,
,
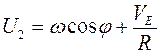 ,
, 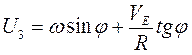 . (3.2)
. (3.2)
Составляющие W1,W2,W3 ускорения точки опоры гироскопа по осям
ξ ζ η равны:

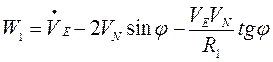 ,
,
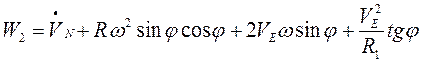 , (3.3)
, (3.3)
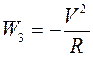 ,
,
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.