Методы совершенствования гирокомпасов двухгироскопнного класса, страница 4

Для применения методов автоматического регулирования необходимо уравнения движения изучаемого прибора представлять в операторной форме.

Для примера представим уравнения движения одногироскопного компаса с непосредственным уравнением, для случая движения судна вдоль меридиана с ускорением  , которые были получены членом-корреспондентом Академии наук СССР профессором Б.В. Булгаковым (5)

 ,                            

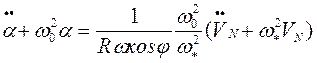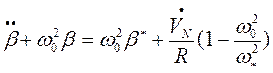                                (3.15)

В этих формулах:

   частота незатухающих колебаний гирокомпаса,

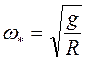  -частота незатухающих колебаний физического маятника, длина нити которого равна радиусу Земли,

,

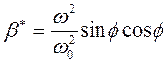        -  угловая скорость вращения Земли.

 Введя в систему (3.15) новые обозначения

- символ дифференцирования,

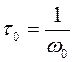- постоянная времени гирокомпаса,

- постоянная времени маятника, частота колебаний которого ,

запишем ее в операторной форме

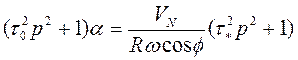,                                                        (3.16)

.

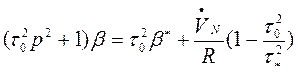Анализ полученных уравнений показывает что невозмущаемость гирокомпаса, функционируещего в режиме незатухающих колебаний, по отношению к ускорению , обеспечивается при соблюдении следующих условий:

1. Из второго уравнения следует , что постоянная времени

гирокомпаса должна быть равной постоянной времени .

Период незатухающих колебаний этого компаса . В этом случае частное решение по координате  от  вообще не зависят.

2. Из первого уравнения следует, что полиномы в правой и левой

частях уравнения должны быть идентичными и одного порядка.

При реализации этих условий полиномы в правой и левой частях

сокращаются и координата от  не зависит

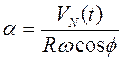 ,                                                                                      (3.17)

.  

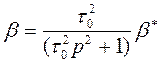Теперь рассмотрим новый метод повышения точности гирогоризонткомпаса при действии на него ускорений, возникающих при маневрировании судна.

Когда гиросфера отклонена от меридиана на угол  сигналы снимаемые с акселерометров определяются приближенными формулами

                                                                

,

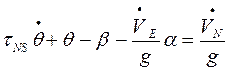
                                                                  (3.18)
 .

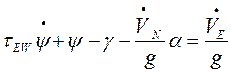Выходные сигналы и акселерометров имеют следующий вид

,

.

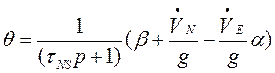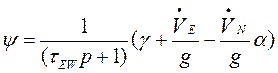Для  существенного уменьшения влияния ускорений  и  на точность КГГК следует откорректировать сигналы  и , используя внешнюю информацию о скорости судна.

Структуру преобразователя управляющих сигналов (ПУС) будем синтезировать опираясь на приближенную формулу

,

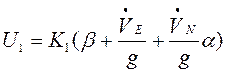где  электрический сигнал на выходе акселерометра.

ПУС должен так преобразовывать сигнал , что бы выходной сигнал не зависел от . Для этой цели подходит апериодическое звено, построенное на интеграторе. Структурная схема этого звена показана на рисунке 3.1.

      

 

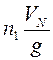
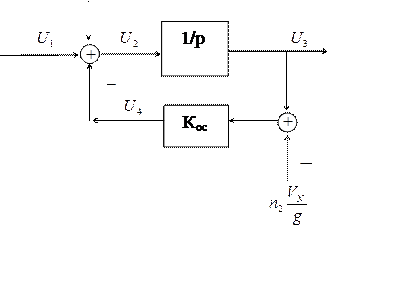                                       Рис. 3.1.

Выходной сигнал   некорректируемого ПУС, имеет такой вид

.

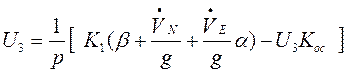После интегрирования это уравнение запишется так

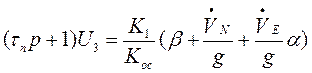,                                                      (3.19)

где 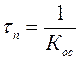- постоянная времени преобразователя сигнала.

Из формулы (3.19) следует, что полезный сигнал  проходит через преобразователь без изменений, но с некоторой задержкой по времени, определяемой постоянной времени .

В выходном сигнале  по прежнему сохранено слагаемое, пропорциональное . Но теперь (3.19) видно, что для того что бы выходной сигнал был свободен от возмущения , необходимо в правой части уравнения, образовать новый полином, идентичный имеющемуся в левой части. Корректирующий работу ПУС сигнал, пропорциональной , может быть подан на любой сумматор. Что бы был выбор подадим корректирующие сигналы на оба сумматора, а именно 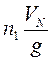   и .

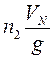Уравнение от корректируемого ПУС принимает следующий вид

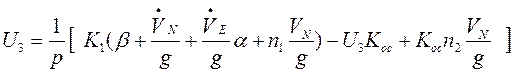.                (3.20)

После интегрирования получаем