Методы совершенствования гирокомпасов двухгироскопнного класса, страница 3

-   стабилизированная сфера и

-   система неподвижного торсионного подвеса гиросферы.

При движении судна постоянной скоростью выходные сигналы и   акселерометров определяются такими формулами:

 ,                                                            (3.7)

.

Сигналы обоих акселерометров используются в КГГК для формирования управляющих моментов, которые налагаются относительно вертикальной и горизонтальноой осей стабсферы.

2. В гиросфере устанавливается кольцевой (двухосный) гидравлический демпфер, движение которого описывается аналогичными (3.7) уравнениями, но имеющими значительно большие постоянный времени

,                                                            (3.8)

.

Кольцевой демпфер может быть применен во всех моделях КГГК. Для повышения точности КГГК при маневрировании судна необходимы выключатели затухания.

3. В КГГК-2, при установке на вертикальных осях гироскопов датчиков моментов, погашение колебаний гиросферы относительно оси  будет обеспечиваться по сигналам акселерометра . Если датчиков моментов не устанавливать, тогда погашение колебаний должно будет выполняться кольцевым гидравлическим демпфером .

С учетом изложенного система уравнений описывающая движение КГГК-2 ( с двумя парами торсионов, без гидравлического демпфера, но с двумя датчиками моментов на гироскопах), запишется так:

,

,

,                                                                                       (3.9)

 ,              

,

,

,

.

где    

, - модули управляющих моментов налагаемых на стабсферу по команде с акселерометра τ_NS,

- корректирующий момент который налагается на гироскопы относительно их вертикальных осей,

- модуль управляющего момента, который налагается относительно оси OZ гиросферы стабилизирующем двигателем по сигналам акселерометра ,

- модуль демпфирующего момента, формируемого обоими датчиками моментов, установленных на гироскопах по сигналам акселерометра.      

В эту систему из восьми уравнений входит 6 неизвестных переменных ,,,,,. Поэтому  2-м переменным можно задать нулевые значения. Устанавливаем, что нулевые значения будут углы  и .Что бы найти значения других частных решений полагаем угловые скорости в системе уравнений  равными нулю, и не учитываются моменты  , , . Тогда другие частные решения принимают такое значение:

,

,

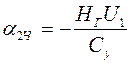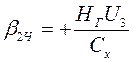 ,                                                                                                          (3.10)

,

,

.

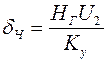      Теперь приступим к определению значений модулей ,

Из пятого и шестого уравнений системы (3.9) находим :

,
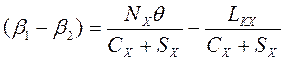
            (3.11)

.

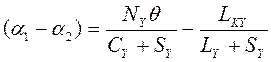Подставив эти формулы в первые  2 уравнения предыдущей системы, получим следующею систему уравнений движения КГГК

,                                

,

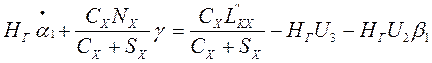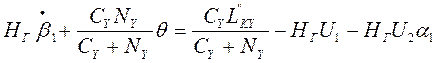,                                                                                  (3.12)

,

,

.   

Обозначив 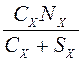=A_Y, 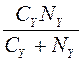   =A_Z, и введя их в уравнения (3.12), находим корректирующие моменты

,                                                                             

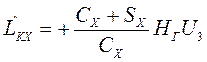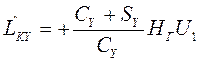,                                                                               (3.13)

.

в которых 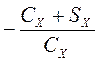 , 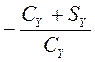являются искомыми передаточными коэффициентами . С учетом корректирующих моментов и неравенства  система (3.7) принимает следующую лаконичную форму записи:

,                                                                 

,                                                (3.14)

   ,                                                                 ,

.

Эту систему уравнений следует принять в качестве базовой для движения судна с постоянной скоростью. Поэтому она должна будет уточняться конкретно для каждой модели при маневрировании судна.

3.3 Применение методов автоматического регулирования к выбору условий невозмущаемости КГГК ускорениями судна.