Термодинамика. Растворы: Методические указания к лабораторным работам по курсу «Физическая химия», страница 19

Данная формула получена методом наименьших квадратов из условия: сумма квадратов отклонений экспериментальных точек от прямой, проходящей через начало координат и имеющей угловой коэффициент, равный , должна быть минимальной. Для расчета  следует заполнить табл. 9.

Таблица 9

К расчету опытного значения криоскопической постоянной

Случайную погрешность величины , найденной методом наименьших квадратов, рассчитывают по формуле

 Опытное значение криоскопической постоянной сравнивают с рассчитанным по уравнению (78). Если разница между  и  не превосходит   , то можно пренебречь систематической погрешностью. В противном случае следует оценить систематическую погрешность δ:

и по формуле (6), приведенной в третьей части «Руководства», определить суммарную погрешность .

Затем требуется оценить целесообразное число значащих цифр в записи результатов измерений и представить результат с указанием погрешности.

Контрольные вопросы

1. Чему равно число степеней свободы при равновесии жидкого раствора с чистым твердым растворителем?

2. Чем определяется величина изменения температуры кристаллизации ΔТ?

3. Для каких растворов наблюдается линейная связь понижения температуры кристаллизации с моляльностью?

4. Каким образом природа растворенного вещества может повлиять на величину изменения температуры кристаллизации?

5. Как измерить температуру кристаллизации в данной работе?

6. От каких факторов зависит криоскопическая постоянная; от каких факторов криоскопическая постоянная не зависит?

ПРИЛОЖЕНИЕ 1. Термодинамические свойства некоторых веществ

ПРИЛОЖЕНИЕ 2. Расчет величины  в работах №1 и №2

Среднюю величину теплового эффекта реакции в изученном интервале температур () можно оценить по опытным значениям константы равновесия при разных температурах. Для этого необходимо проинтегрировать уравнение изобары химической реакции, считая  постоянным:

,

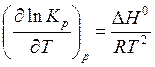после интегрирования получим

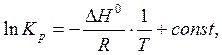
где  – постоянная интегрирования. Из данного соотношения следует, что опытные данные, представленные в координатах «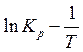», должны располагаться около прямой линии, угловой коэффициент которой  равен .

Следовательно,

При нахождении углового коэффициента необходимо учесть, что масштаб оси абсцисс и оси ординат различен. Поэтому  следует находить как отношение катетов прямоугольного треугольника, длины которых выражены в единицах соответствующих осей.

Таким образом,

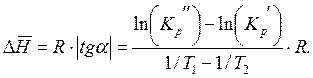
ПРИЛОЖЕНИЕ 3. Интегральные теплоты растворения некоторых солей в воде при 25ºС

Библиографический список

1.  Жуховицкий А.А. Физическая химия / А.А. Жуховицкий, Л.А, Шварцман. М.: Металлургия, 2001. 688с.

2.  Стромберг А.Г. Физическая химия / А.Г. Стромберг, Д.П. Семченко. М.: Высшая школа, 1988. 496 с.

3.  Карапетьянц М.Х. Химическая термодинамика / М.Х. Карапетьянц, М.: Химия, 1985. 580 с.

4.  Краткий справочник физико-химических величин/ Под ред. А.А. Равделя и А.М. Пономаревой. СПб: Медный всадник, 2003. 240 с.

5.  Зайдель А.Н. Погрешности измерений физических величин. Л.: Наука, 1985. 112 с.