Термодинамика. Растворы: Методические указания к лабораторным работам по курсу «Физическая химия», страница 16

Допустим, эта зависимость для молярного объема известна и представлена на рис. 10.

Докажем, что отрезок Оа, отсекаемый касательной AM, проведенной к кривой  в точке М, численно равен парциально-молярному объему первого компонента в растворе состава .Из рисунка следует, что для любой выбранной мольной доли второго компонента (), в том числе и для , справедливо равенство:

В бинарном растворе

a , т.к. . 

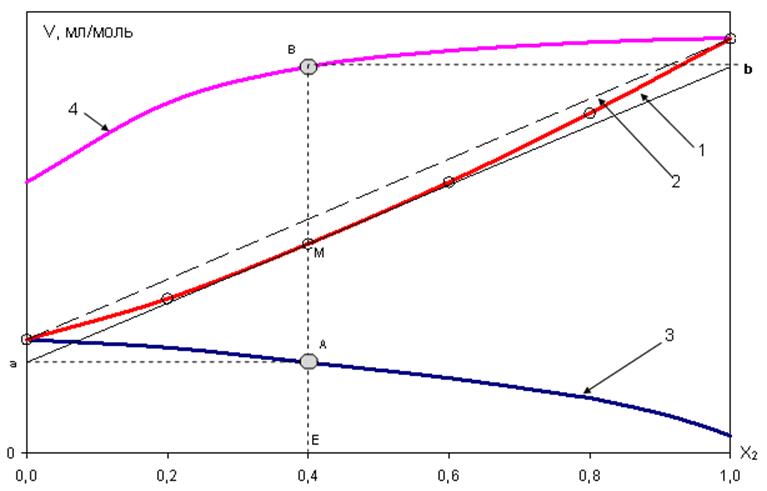
Рис. 10 – к определению парциально-молярных объемов раствора

Учитывая это обстоятельство и соотношение (57), запишем равенство (58) в виде:

Таким образом, отрезок Оа, отсекаемый касательной на оси ординат при , равен парциально-молярному объему первого компонента. Аналогично отрезок, отсекаемый этой касательной аb на оси ординат справа, то есть при , соответствует величине   .

Кривая  на рис. 10 проходит ниже аддитивной прямой (пунктир), характерной для идеальных растворов, где

Причиной отклонения молярного объема реального раствора от такового для идеального является различие в энергиях связи между различными частицами раствора. Если энергия   связи разноименных частиц (  ) больше средней энергии связи одноименных (), то есть

и образование раствора сопровождается его уплотнением.

Подобная зависимость характерна для растворов с отрицательными отклонениями от идеального раствора. При значительных различиях в энергиях связи парциально-молярный объём компонента может оказаться отрицательным, что говорит об уменьшении общего объема раствора при добавлении к нему данного компонента.

Порядок выполнения работы

 Молярный объем раствора можно найти из очевидного соотношения

в котором  – молярные массы компонентов раствора, а  – плотность раствора.

Плотность раствора , необходимую для расчета молярного объема , можно определить методом взвешивания металлического шарика последовательно на воздухе, в чистой воде и в данном водном растворе. Для этой цели в работе используются аналитические весы, к одному из коромысел которых подвешен металлический грузик (I) объемом около 1см³ (см. рис. 11).

При взвешивании, шарика объемом  и плотностью , находящегося в какой-либо среде (воздух, вода, раствор) плотностью , следует учесть выталкивающую силу Архимеда , поэтому измеряемый вес в среде ()

Записывая уравнение (64) для трех сред (воздух, вода и раствор), получим систему трех уравнений с тремя неизвестными величинами (). Её решение дает следующую расчетную формулу для плотности раствора:

Поскольку плотность воздуха мала и составляет при нормальных условиях 0,0013 г/см³, а множитель, стоящий после нее в уравнении (65), значительно меньше единицы, то для практических расчетов целесообразно воспользоваться формулой

Взвешивание шарика в растворе проводится три раза по схеме: колба №1, №2, №3, ... ; №1, №2, №3 ... ; №1, №2, №3 ... ; Результаты взвешивания вносят в табл. 6.

Таблица 6

Результаты взвешивания

По результатам трех взвешиваний по формуле (4) согласно пункту 2 на стр. 8  руководства «Термодинамика» следует найти случайную среднеквадратическую погрешность определения молярного объема (), затем определить относительную погрешность измерения величин . По этим данным оценить целесообразное  число значащих цифр в результате и заполнить колонку  табл. 7.

Таблица 7

Результаты определения величин