Ионные свойства связи. Метод молекулярных орбиталей, двухатомные молекулы, страница 9

Здесь l ¹ ± 1. Энергии МО вычисляются аналогично случаю с гомоядерными двухатомными молекулами, путём решения вековых уравнений второй степени.     Вместе с тем, с помощью условий, упомянутых ранее для  образования гомоядерных молекул (близость энергий, максимальное перекрывание, согласованные свойства симметрии), легко указать какие АО  y_А и y_В  могут комбинировать между собой. Кроме того, сохраняет прежний смысл классификация МО по типам симметрии (s, p), а также степень вырождения МО. Остаётся справедливым и правило непересечения, согласно которому уровни энергии МО одинаковой симметрии взаимно отталкиваются. И для гетероядерных молекул можно построить корреляционную диаграмму. Основное отличие её от соответствующей диаграммы для гомоядерных молекул: 1) В отсутствии свойств чётности (g и u), что связано с потерей центральной симметрии. 2) В различии энергий одинаковых орбиталей у разделённых атомов. Например, в молекуле NO связывающая МО s2s коррелирует с АО кислорода 2s, а разрыхляющая МО s^*2s – с АО 2s азота, так как вследствие большего ядерного заряда энергетические уровни кислорода ниже соответствующих уровней азота. Образование молекулы NO из атомов N и О можно представить следующим образом:

N[1s²2s²2p³] + O[1s²2s²2p⁴] ® NO[KK(zs)²(ys)²(xs)²(wp)⁴(vp)] .

Эта молекула имеет один неспаренный электрон, поэтому она парамагнитна (её терм ²P).

8.10. Полярность орбиталей.

          Для гетерополярной МО соответствует волновая функция

Y = y_А + ly_В.                                                                                  (8.7)

Если ½l½ > 1, то можно сказать, что y_В вносит более существенный вклад в МО, чем y_А, т.е. электронная плотность вблизи В больше, чем вблизи А. Соответствующая МО у ядра В имеет большую толщину, чем у ядра А. Очевидно, что l характеризует полярность орбитали и, следовательно, связана с величиной дипольного момента молекулы. Расчёты l весьма ненадёжны. Поэтому обычно l вычисляют из экспериментальных значений дипольного момента. Соотношение между l и дипольным моментом вытекает из следующих соображений. Плотность r зарядового облака электрона, находящегося на орбитали пропорциональна

,

где нормировочный множитель N определяется соотношением

.

Среднее значение координаты  центра тяжести (от середины прямой, соединяющей атомы А и В) зарядового облака вычисляется:

,                                                          

где R - расстояние между ядрами молекулы, а множитель x_AB  обычно очень мал и им пренебрегают. В этом случае распределение двух электронов на МО таково, что их центр “тяжести” находится на расстоянии

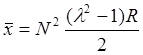
от средней точки молекулярной оси. Отсюда величина дипольного момента равна

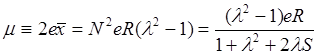.                                                      (8.8)

Данное соотношение, связывающее m и l, можно применять, если рассматриваемые два электрона являются единственными связывающими электронами и если поляризация, обусловленная другими не связывающими электронами мала.

Таблица 8.3. Значение коэффициента l в выражении МО y_А + ly_В, вычисленные из экспериментальных данных о дипольных моментах по уравнению 8.8.

Видно, что для всех представленных в таблице галоидов l > 1. Однако, за исключением очень полярных молекул (HF, KCl) l не намного превышает единицу. Существует ещё другая, более простая, но несколько менее точная интерпретация выражения 8.7. Полагают, что атомные орбитали y_А и y_В входят в полную волновую функцию с относительными весами , вследствие чего часть электронного заряда, равная 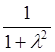, находится вблизи ядра А, а часть, равная 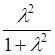, - вблизи ядра В. Если предположить, что центры “тяжести” этих зарядов совпадают с ядрами, то дипольный момент, обусловленный двумя электронами с таким распределением и положительными ядерными зарядами, будет равен