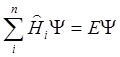Ионные свойства связи. Метод молекулярных орбиталей, двухатомные молекулы, страница 3

          ,

где

          .

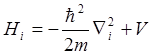          В соответствии с методом МО:

          1) Каждому электрону в молекуле соответствует некоторая волновая функция Y, которую можно назвать молекулярной орбиталью, т.к. она определяет движение (орбиту) электрона в молекуле. Молекулярные орбитали в отличие от атомных орбиталей являются многоцентровыми. Величина Y²dt равна вероятности нахождения электрона в объёме dt. Соответственно плотность зарядового облака молекулярной орбитали r = еY².

          2) Каждая волновая функция, как и в случае атомных орбиталей, характеризуется тремя квантовыми числами, от которых зависит её форма, энергия соответствующего уровня, свойства симметрии, кратность вырождения. Каждый электрон в МО (как и в случае атома) характеризуется и спиновым квантовым числом S = ± 1/2.

          3) Каждой волновой функции соответствует определённая энергия (собственное значение оператора Гамильтона, тесно связанное с энергией, необходимой для удаления электрона из молекулы в бесконечность). Полная энергия складывается из кинетической энергии, потенциальной энергии притяжения к ядрам и энергии межэлектронного отталкивания.

          4) Электронная структура молекулы устанавливается по определённому принципу. Сначала определяются дозволенные орбитали. Затем в соответствии с принципом исключения Паули и правилом Гунда на них размещаются электроны.

          8.2. Приближение ЛКАО.                                                             

          Одним из широко используемых способов приближённого описания волновой функции электрона в молекуле служит выражение МО в виде линейной комбинации атомных орбиталей (ЛКАО). Молекулярная орбиталь двухатомной молекулы AB является двухцентровой, т.е. электрон в молекуле движется по орбите, проходящей вблизи обоих ядер. На электрон, находящийся вблизи от одного из ядер действуют силы главным образом со стороны этого ядра (и находящихся около него глубинных атомных электронов). В области ядра А волновая функция сводится к волновой функции изолированного атома y_a, а в области ядра B – y_b. Воспользовавшись методом линейных комбинаций, для МО одного электрона получим следующую волновую функцию:

.                                                                                   (8.1)

Для молекулы с двумя электронами:

.                                                (8.2)

Значения коэффициентов выбираются в соответствии с принципом Ритца, т.е. с условием минимума энергетической функции

.                                    

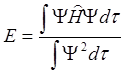          Чтобы комбинация y_a и y_b была эффективной, необходимо выполнение условий, аналогичных условиям образования связи по методу валентных связей:

          - энергии, соответствующие y_a и y_b были сравнимы по величине;

          - зарядовые облака еy_a² и еy_b² по возможности полнее перекрывались;

          - y_a и y_b обладали одинаковыми свойствами симметрии относительно молекулы АВ.

          Если указанные условия не выполняются, то y_a и y_b комбинируют между собой лишь в незначительной степени.

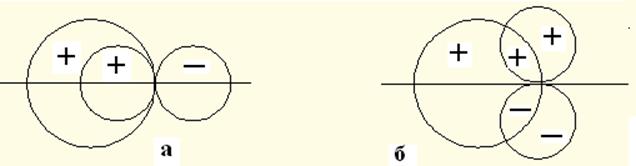
          Рис.8.1. Схема взаимодействия y_a и y_b: а – s и р_х; б – s и р_z.

Важным условием образования молекулярной орбитали является соответствие симметрии волновых функций y_a и y_b. Это связано с тем, что, если волновая функция s-электрона положительна, то волновые функции p- и d-электронов имеют симметричные составляющие разных знаков. Возможно такое сочетание симметрий, при котором интегралы перекрывания будут равны нулю. В этом случае свойства симметрии орбиталей y_a и y_b препятствуют построению из них молекулярной орбитали. На рис.8.1 представлены случаи сочетания разных симметрий: разрешающие (а) и запрещающие (б) образование молекулярной орбитали. Видно, что при совпадении осей молекулы и р-функции образование связи возможно, а  при их перпендикулярном расположении интеграл перекрывания равен нулю и связь не возможна.  В табл.8.1 представлены разрешённые и запрещённые по симметрии сочетания волновых функций для различных состояний электронов. Например, в случае образования молекулы HCl энергия орбиталей хлора 1s, 2s, 2p и 3s ниже, чем 1s-электрона атома водорода. Близкими по энергии к  1s-электрону атома водорода будет 3р-орбиталь хлора. Но из-за того, что р_y- и р_z-состояния заполнены полностью, то в образовании связи принимает участие неспаренный 3р_х-электрон. Т.о. электрон, первоначально находившийся в состоянии y_a, и электрон, находившийся в состоянии y_b, при спаривании переходят в молекулярное состояние Y = y_a + ly_b.