В основе всех понятий изучаемых в различных разделах алгебры лежит понятие алгебраической операции.
Пусть ![]() – множество (элементами
– множество (элементами
![]() могут быть числа или функции или объекты
геометрической природы и т.д.).
могут быть числа или функции или объекты
геометрической природы и т.д.).
Говорят, что на ![]() задана бинарная
алгебраическая операция, если любой упорядоченной паре
задана бинарная
алгебраическая операция, если любой упорядоченной паре ![]() элементов
элементов ![]() ставится в соответствие однозначно
определённый элемент
ставится в соответствие однозначно
определённый элемент ![]() этого же множества
этого же множества ![]() .
.
Иногда вместо ![]() пишут
пишут ![]() , а ещё чаще бинарную операцию на
, а ещё чаще бинарную операцию на ![]() обозначают каким-нибудь специальным
символом: *, º, ∙, +, так будем поступать и мы, называя
обозначают каким-нибудь специальным
символом: *, º, ∙, +, так будем поступать и мы, называя ![]() (или просто
(или просто ![]() , без
знака между
, без
знака между ![]() и
и ![]() ) произведением
элементов
) произведением
элементов ![]() . Таким образом, равенство
. Таким образом, равенство
![]() (1)
(1)
будет в дальнейшем иметь следующий смысл:
упорядоченной паре ![]() из
из ![]() ставится
в соответствие элемент
ставится
в соответствие элемент ![]() . Иногда (там, где это будет
удобнее) вместо «произведение» будем говорить «сумма», обозначая это так:
. Иногда (там, где это будет
удобнее) вместо «произведение» будем говорить «сумма», обозначая это так:
![]() (1´)
(1´)
( конечно, во многих случаях названия «сумма» и «произведение» условны)
Замечание 1. Можно
рассматривать бинарную операцию в «широком смысле»: некоторым
упорядоченным парам элементов из ![]() ставится
в соответствие элемент из
ставится
в соответствие элемент из ![]() один или много.
Такой, более общий подход «имеет право на существование», он приводит к
интересным результатам, однако мы, исходя из наших целей, будем придерживаться
понятия алгебраической операции приведённого выше.
один или много.
Такой, более общий подход «имеет право на существование», он приводит к
интересным результатам, однако мы, исходя из наших целей, будем придерживаться
понятия алгебраической операции приведённого выше.
Замечание 2. Наряду с бинарными алгебраическими операциями имеет смысл рассматривать и более общие n-арные операции(унарные при n=1, тернарные при n=3 и т.д.), а также и их комбинации.[1] Нас же будут интересовать, за редкими исключениями, именно бинарные операции.
На множестве ![]() можно задать много различных операций.
Если хотят выделить одну из них, то пишут
можно задать много различных операций.
Если хотят выделить одну из них, то пишут ![]() и
говорят, что операция * определяет на
и
говорят, что операция * определяет на ![]() алгебраическую
структуру или, что
алгебраическую
структуру или, что ![]() - алгебраическая структура (другое
название: алгебраическая система).
- алгебраическая структура (другое
название: алгебраическая система).
Примеры.
1. На множестве целых чисел
определены операции сложения и умножения. Таким образом, заданы алгебраические
структуры ![]() и
и ![]() .
.
2. На ![]() можно задать и другие операции:
можно задать и другие операции: ![]() ;
; ![]() ,
получим структуры
,
получим структуры ![]() и
и ![]() и т.д.
и т.д.
3. На множестве ![]() невырожденных матриц порядка n (
невырожденных матриц порядка n (![]() ): а) матричное умножение –
алгебраическая операция, б) матричное сложение – нет.
): а) матричное умножение –
алгебраическая операция, б) матричное сложение – нет.
Доказательство:
а) Пусть ![]() и
и ![]() - две
невырожденные матрицы n-го порядка:
- две
невырожденные матрицы n-го порядка: ![]() ,
, ![]() .
Матрица
.
Матрица ![]() - снова матрица n-го
порядка, осталось доказать лишь её невырожденность. Поскольку, как известно,
определитель произведения матриц равен произведению определителей этих матриц,
т.е.
- снова матрица n-го
порядка, осталось доказать лишь её невырожденность. Поскольку, как известно,
определитель произведения матриц равен произведению определителей этих матриц,
т.е. ![]() , то
, то ![]() . Итак,
матрица
. Итак,
матрица ![]() является элементом того же множества, что
и матрицы
является элементом того же множества, что
и матрицы ![]() и
и ![]() .
.
б) Достаточно привести пример двух таких невырожденных матриц, сумма которых является вырожденной матрицей.
Пусть 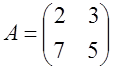 ,
, 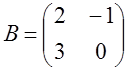 .
Тогда
.
Тогда ![]() ,
, ![]() ,
, 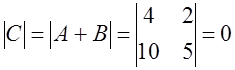 .
.
4. ![]() .
Сложение не является бинарной алгебраической операцией (объясните, почему).
.
Сложение не является бинарной алгебраической операцией (объясните, почему).
5. Рассмотрим множество векторов на плоскости. Скалярное произведение векторов не является алгебраической операцией (почему?).
6. Рассмотрим множество векторов на плоскости и определим сложение векторов по «правилу треугольника». Это – алгебраическая операция.
7. Векторное произведение векторов – алгебраическая операция.
Конструировать разные бинарные
операции на множестве ![]() можно неограниченно, но
задача изучения произвольных алгебраических структур слишком обща.
Поэтому рассматривают структуры при некоторых естественных ограничениях.
можно неограниченно, но
задача изучения произвольных алгебраических структур слишком обща.
Поэтому рассматривают структуры при некоторых естественных ограничениях.
Чаще всего нас будет интересовать выполнимость ассоциативного и коммутативного законов для операции.
Бинарная операция * на множестве ![]() называется ассоциативной, если
называется ассоциативной, если ![]() для всех
для всех ![]() .
.
Операция * называется коммутативной,
если ![]() для всех
для всех ![]() .
.
Свойства ассоциативности и
коммутативности независимы. Действительно, например операция на ![]() :
: ![]() является
коммутативной (очевидно), но не ассоциативной, что легко показать:
является
коммутативной (очевидно), но не ассоциативной, что легко показать: ![]() , а
, а ![]() .
Операция же умножения квадратных матриц порядка
.
Операция же умножения квадратных матриц порядка ![]() -
ассоциативна, но не коммутативна.
-
ассоциативна, но не коммутативна.
Примеры.
1. Операции сложения и
умножения на множестве ![]() действительных чисел
коммутативны и ассоциативны.
действительных чисел
коммутативны и ассоциативны.
2. Операция * на множестве
натуральных чисел, задаваемая формулой ![]() -
некоммутативна (например
-
некоммутативна (например ![]() ,
, ![]() ).
).
3. Операция на множестве ![]() , заданная формулой
, заданная формулой 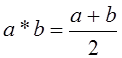 -
коммутативна, но не ассоциативна.
-
коммутативна, но не ассоциативна.
Доказательство:
Пусть ![]() - любые
действительные числа. В силу коммутативности сложения на
- любые
действительные числа. В силу коммутативности сложения на ![]() получим:
получим: 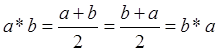 , и
коммутативность операции * доказана.
, и
коммутативность операции * доказана.
Далее, 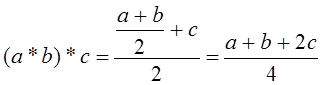 ,
и
,
и 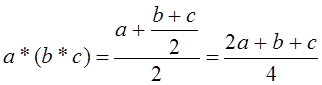 , и при
, и при ![]() равенство
равенство
![]() не верно.
не верно.
Пусть на множестве ![]() задана бинарная операция. Если существует
такой элемент
задана бинарная операция. Если существует
такой элемент ![]() , что для любого элемента
, что для любого элемента ![]() выполняются равенства:
выполняются равенства:
![]() и
и ![]() ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.