Алгебраическая операция. Коммутативные и ассоциативные операции. Смежные классы по подгруппе. Теорема Лагранжа, страница 7

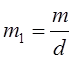Все вычеты из (4) и только они удовлетворяют сравнению (3) и равносильному ему сравнению . По модулю  все числа из (4) принадлежат одному классу. По модулю  они принадлежат различным классам:

       

Следовательно, сравнение  имеет  решений:

, ,…, .

Пример. . Так как , , то сравнение имеет 3 решения. Делим обе части и модуль на 3, получаем: . Решениями сравнения  будут: , , .

Пример. . Т.к. , , то сравнение имеет 3 решения. После деления обеих частей и модуля на 3 получим сравнение:

. Решение этого сравнения: .

Решения заданного сравнения: , , .

Порядок класса вычетов. Первообразные корни. Индексы.

1. Порядок класса вычетов.

Изучим подробнее строение группы , состоящей из обратимых элементов в кольце вычетов . Эта группа состоит из классов вычетов взаимно простых с модулем  и содержит  классов вычетов.

Так как умножение в кольце  коммутативно, то - коммутативная группа, состоящая из  элементов. Поэтому все элементы  группы  (т.е. все классы вычетов по модулю , взаимно простые с ) имеют конечный порядок и этот порядок – делитель (это следует из теоремы Лагранжа). Учитывая определение порядка элемента в группе, получаем следующее определение порядка класса вычетов:

Определение 1. Порядком класса вычетов , взаимно простого с модулем , называется наименьшее натуральное число , такое, что .

Число  называют также порядком всех чисел , входящих в класс вычетов . Если , то из равенства  следует, что . Итак, получаем следующее:

Определение 2. Пусть число  взаимно просто с , .

Порядком числа  по модулю  называется наименьшее натуральное число , такое, что .

Если порядок класса вычетов  (соответственно числа ) по модулю  равен , то  называется показателем  (числа ) по модулю , или что () принадлежит показателю  по модулю .

Если порядок класса вычетов  по модулю  равен , то циклическая подгруппа, порождённая классом вычетов  в группе , состоит из  элементов. И можно применить к этой подгруппе все результаты о циклических подгруппах (см…..).

В частности, имеет место:

Теорема 1. Если  и порядок  по модулю  равен , то  тогда и только тогда, когда  делится на .

Следствие 1. Если порядок класса вычетов  по модулю  равен , то  тогда и только тогда, когда , т.е  делится на .

Следствие 2. Если порядок класса вычетов  по модулю  равен , то все классы вычетов  различны.

Теорема 2. Если порядок класса вычетов  по модулю  равен , то порядок класса вычетов  равен .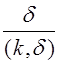

Следствие. Если порядок класса вычетов  по модулю  равен , то среди классов вычетов  порядок  имеют  классов.

Доказательство. По следствию 2 из теоремы 1 все классы вычетов  различны. Порядок  имеют те из этих классов, для которых . Число таких классов равно .

Пример. Найдём  порядок класса вычетов  по модулю , а также все классы вычетов по этому модулю, порядок которых равен порядку класса вычетов

Порядок любого класса вычетов является делителем числа , следовательно порядок класса вычетов  по модулю  - это делитель числа . Натуральные делители числа  - числа . Будем возводить число  в степени с показателями  до тех пор, пока не получим число, сравнимое с  по модулю . Имеем: , , , . Итак, порядок числа 7 по модулю 43 равен 6

Чтобы найти остальные классы вычетов по модулю 43, имеющие порядок 6, рассмотрим числа 0,1,2,3,4,5. Выбираем из них взаимно простые с , т.е 1 и 5. Значит, искомые классы вычетов:  и . Но . Получили: искомые классы вычетов  и .

2. Первообразные корни по простому модулю.

Пусть  - простое число. Группа  обратимых элементов кольца  состоит из классов вычетов . По теореме 1 порядок каждого из этих классов вычетов является делителем числа .

Определение 3. Первообразным корнем по простому модулю  называется класс вычетов  по этому модулю, порядок которого равен .

По следствию 2 из теоремы 1 получаем: если  - первообразный корень по простому модулю , то все степени  различны (в этом случае ).