Алгебраическая операция. Коммутативные и ассоциативные операции. Смежные классы по подгруппе. Теорема Лагранжа, страница 3

3.     Пусть  – группа всех подстановок степени 3, выделим в ней подмножество  из подстановок:

,  .

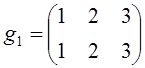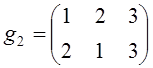        Легко проверить (упражнение), что , , . Таким образом, произведения элементов из  снова принадлежат , т. е. условие 1) выполнено. Кроме того, равенства  и  показывают, что каждый из элементов ,  является обратным самому себе. Значит, выполнено и условие (2). Следовательно, подмножество  является подгруппой группы .

        Совокупность условий (1) и (2) можно заменить следующим  одним условием:

3) Для любых двух элементов  и  элемент  принадлежит .

        Доказательство. Если выполнены условия 1) и 2), то 3) выполняется. С другой стороны, если имеет место 3), то, взяв произвольный элемент , получим: , т. е. . Но тогда , т. е. выполнено 2). Пусть теперь  и . Тогда , и, следовательно, . Таким образом, из (3) следует и (1).

Смежные классы по подгруппе. Теорема Лагранжа.

        Пусть  и  – два каких-либо подмножества группы . Определим произведение подмножеств  и  как совокупность всевозможных произведений , где , а . Будем обозначать это произведение символом . Итак, по определению:

.

        Примеры.

а)     , ; . Произведением  будет интервал .

б)     Снова , ; 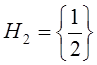. Теперь .

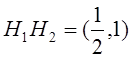        Замечание. Мультипликативная терминология здесь используется по традиции. В некоторых примерах предпочтительнее использовать аддитивную терминологию, говоря о сумме подмножеств, обозначая ее символом . Вообще, под произведением элементов  и  понимается композиция их  в смысле операции на  , поэтому произведение множеств ,  естественно было бы обозначать  и называть композицией этих множеств. Особо отметим, что определенное выше произведение нельзя смешивать с их теоретико-множественным произведением!

        Покажем, что операция умножения подмножеств группы ассоциативна. Ввиду ассоциативности операции в группе  для любых трех элементов  имеет место равенство , а это означает, что подмножества  и  состоят из одних и тех же элементов, т. е. .

        Пусть теперь  – некоторая подгруппа группы , а  – произвольный элемент этой группы. Произведение  подгруппы  и одноэлементного множества  назовем правым смежным классом элемента  по подгруппе . Обозначение: . Таким образом, правый смежный класс элемента  по подгруппе  есть множество произведений всех элементов из  на элемент  справа. Аналогично, левый смежный класс элемента  по подгруппе  определяется как , т. е. как совокупность всех произведений вида , где  и обозначается . В случае абелевой группы  для любых элементов  и  имеет место равенство , поэтому , т. е. левый смежный класс и правый смежный класс любого элемента  по любой подгруппе  совпадают. В случае произвольной группы левый и правый классы одного и того же элемента могут не совпадать.

        Для любого элемента  из подгруппы  класс  совпадает с  (упражнение – доказать). Отсюда следует, что если , т. е. , где , то H. Таким образом, всякий правый класс совпадает с правым классом любого своего элемента.

Теорема.Какова бы ни была подгруппа  группы . Совокупность всех различных правых (левых) смежных классов по подгруппе  образует разбиение группы .

Доказательство.Будем доказывать теорему для правых классов – доказательство для левых классов аналогично. Каждый элемент  принадлежит некоторому классу, а именно, классу  (единица  группы  содержится в , поэтому ) значит объединение классов совпадает с . Покажем, что если бы два какие-нибудь класса имеют хотя бы один общий элемент, то они совпадают. Действительно, если   и , то  и ,откуда . Итак, любые два класса либо не пересекаются, либо совпадают.

Следствие(теорема Лагранжа). Порядок конечной группы делится на порядок любой ее подгруппы.                                    

Доказательство. Пусть конечная группа  имеет порядок ,  – ее подгруппа порядка .Обозначим элементы  так: . Для любого  правый  класс  состоит из элементов  , которые все различны (если ,то . Значит, каждый класс содержит  элементов. Пусть имеется всего  различных классов. Обозначим их . По теореме получаем: , т.е. группа , состоящая из  элементов, разбивается на  непересекающихся классов по  элементов в каждом. Следовательно, , значит  делится на .