то элемент ![]() называется
нейтральным относительно данной операции (другое название – единичный
элемент).
называется
нейтральным относительно данной операции (другое название – единичный
элемент).
Примеры.
1. Число 1 является
нейтральным элементом множества ![]() относительно
операции умножения.
относительно
операции умножения.
2. Матрица 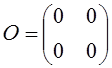 - нейтральный элемент множества всех
матриц второго порядка относительно операции сложения матриц.
- нейтральный элемент множества всех
матриц второго порядка относительно операции сложения матриц.
3. Множество натуральных
чисел не имеет нейтрального элемента относительно операции, задаваемой формулой
![]() , т.к. иначе для некоторого числа
, т.к. иначе для некоторого числа ![]() и любого
и любого ![]() выполнялись
бы равенства:
выполнялись
бы равенства: ![]() и
и ![]() , что
невозможно.
, что
невозможно.
Эти примеры показывают, что может существовать один нейтральный элемент и что нейтрального элемента может не быть вовсе. Оказывается, других возможностей нет, т.е. не может быть более одного нейтрального элемента.
Доказательство:
Пусть ![]() и
и ![]() - два нейтральных элемента относительно
операции *. Тогда
- два нейтральных элемента относительно
операции *. Тогда ![]() (т.к
(т.к ![]() -
нейтральный элемент), и
-
нейтральный элемент), и ![]() (т.к
(т.к ![]() - нейтральный элемент), откуда
- нейтральный элемент), откуда ![]() .
.
Пусть теперь множество ![]() содержит
нейтральный элемент
содержит
нейтральный элемент ![]() относительно некоторой бинарной
операции *. Элемент
относительно некоторой бинарной
операции *. Элемент ![]() называется правым обратным
для элемента
называется правым обратным
для элемента ![]() , если
, если ![]() ,
элемент
,
элемент ![]() называется левым обратным для
называется левым обратным для ![]() , если
, если ![]() . Если
операция ассоциативна, то левый и правый обратные элементы совпадают.
. Если
операция ассоциативна, то левый и правый обратные элементы совпадают.
Доказательство:
![]() (2)
(2)
![]() (3)
(3)
Умножим равенство (2) слева на ![]() :
: ![]()
По ассоциативности: ![]() ,
,
из (3) следует: ![]() , но
, но ![]() , а
, а ![]() , значит
, значит
![]() .
.
Таким образом, в случае ассоциативной операции можно говорить просто об обратном элементе.
Обозначение: ![]() . Ясно, что
. Ясно, что ![]() .
.
Примеры.
1. Рассмотрим операцию умножения на множестве ![]() действительных чисел. Нейтральный элемент
– число 1. Если
действительных чисел. Нейтральный элемент
– число 1. Если ![]() , то обратный элемент
, то обратный элемент 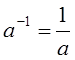 существует. Для числа 0 обратного нет.
Если рассматривать операцию умножения только на множестве
существует. Для числа 0 обратного нет.
Если рассматривать операцию умножения только на множестве ![]() положительных действительных чисел, то все
элементы будут иметь обратные.
положительных действительных чисел, то все
элементы будут иметь обратные.
2. Множество ![]() с
операцией сложения. Каждый элемент
с
операцией сложения. Каждый элемент ![]() имеет обратный, равный
имеет обратный, равный ![]() .
.
3. Множество квадратных матриц второго порядка с операцией матричного умножения. Каждая невырожденная матрица обладает обратной, а для вырожденной матрицы обратной не существует.
Рассмотренные примеры показывают, что некоторые элементы обладают обратными, но могут существовать и элементы, не имеющие обратных. Естественно возникает вопрос: может ли какой-нибудь элемент обладать несколькими обратными? В рассмотренных примерах все элементы имели не более одного обратного, и это не случайно, т.к справедливо утверждение:
Если операция ассоциативна, то никакой элемент не может иметь более одного обратного.
Доказательство:
Пусть ![]() и
и ![]() - обратные элементы для элемента
- обратные элементы для элемента ![]() . Тогда
. Тогда ![]() и
и ![]() (совпадение левого и правого обратных уже
доказано).
(совпадение левого и правого обратных уже
доказано).
Теперь получаем:
![]()
![]()
![]()
![]()
![]()
Пусть множество ![]() является
группой относительно некоторой бинарной операции. Подмножество
является
группой относительно некоторой бинарной операции. Подмножество ![]() множества
множества ![]() , являющееся группой относительно той же
операции, называется подгруппой группы
, являющееся группой относительно той же
операции, называется подгруппой группы ![]() .
.
Непосредственно из определения следует, что всякая группа
является своей подгруппой, и что множество, состоящее из одного элемента –
единицы группы, также будет ее подгруппой. У группы могут быть и другие
подгруппы. Подгруппа ![]() называется собственной,
если
называется собственной,
если ![]() и
и ![]() .
.
Примеры.
1. Множество положительных рациональных чисел ![]() является группой относительно операции
умножения и поэтому подгруппой мультипликативной группы положительных
действительных чисел.
является группой относительно операции
умножения и поэтому подгруппой мультипликативной группы положительных
действительных чисел.
2. Множество целых чисел ![]() , будучи
группой относительно сложения, составляет подгруппу аддитивной группы
действительных чисел.
, будучи
группой относительно сложения, составляет подгруппу аддитивной группы
действительных чисел.
Чтобы установить, что непустое множество ![]() группы
группы ![]() есть
подгруппа этой группы, достаточно проверить два условия:
есть
подгруппа этой группы, достаточно проверить два условия:
1) Для любых двух элементов ![]() ,
, ![]() их композиция
их композиция ![]() принадлежит
принадлежит
![]() .
.
2) Для любого элемента ![]() обратный
ему элемент
обратный
ему элемент ![]() также принадлежит
также принадлежит ![]() .
.
Докажем это. Условие (1) означает, что операция на множестве
![]() будет операцией и на множестве
будет операцией и на множестве ![]() . Ассоциативность операции на
. Ассоциативность операции на ![]() следует из ее ассоциативности на
следует из ее ассоциативности на ![]() . Из условий (1) и (2) следует, что
. Из условий (1) и (2) следует, что ![]() : взяв какой-либо элемент
: взяв какой-либо элемент ![]() , по условию (2) найдем в
, по условию (2) найдем в ![]() обратный ему элемент
обратный ему элемент ![]() , а по условию (1) получим, что
, а по условию (1) получим, что ![]() содержится в
содержится в ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.