Определение 1. Целое число ![]() называется общим делителем целых
чисел
называется общим делителем целых
чисел ![]() , если каждое из этих чисел делится на
, если каждое из этих чисел делится на ![]() .
.
Определение 2. Целое число ![]() называется наибольшим общим делителем
чисел
называется наибольшим общим делителем
чисел ![]() , если :
, если :
1) ![]() является общим делителем этих
чисел;
является общим делителем этих
чисел;
2) ![]() делится на любой общий делитель
чисел
делится на любой общий делитель
чисел ![]() .
.
Теорема 1. Наибольший общий делитель чисел ![]() определён однозначно с точностью до знака
(т.е. если
определён однозначно с точностью до знака
(т.е. если ![]() и
и ![]() наибольшие
общие делители чисел
наибольшие
общие делители чисел ![]() , то либо
, то либо ![]() ,
либо
,
либо ![]() )
)
Доказательство. Пусть ![]() и
и
![]() - наибольшие общие делители чисел
- наибольшие общие делители чисел ![]() . Т.к.
. Т.к. ![]() -
наибольший общий делитель, то он делится на любой общий делитель этих чисел, в
частности на
-
наибольший общий делитель, то он делится на любой общий делитель этих чисел, в
частности на ![]() , т.е.
, т.е. ![]() . Точно
так же получаем, что
. Точно
так же получаем, что ![]() . Но тогда
. Но тогда ![]() ,
, ![]() -
целое, и
-
целое, и ![]() , поэтому
, поэтому ![]() , и
аналогично,
, и
аналогично, ![]() . Но эти неравенства одновременно имеют
место лишь в случае
. Но эти неравенства одновременно имеют
место лишь в случае ![]() .
.
Условимся всегда рассматривать положительное значение
наибольшего общего делителя чисел ![]() . Обозначение:
. Обозначение: ![]() .
.
Пример. ![]() .
Действительно, множество положительных делителей числа 135 есть
.
Действительно, множество положительных делителей числа 135 есть ![]() , а для числа –180 такое множество имеет
вид
, а для числа –180 такое множество имеет
вид ![]() . Пересечение этих множеств
. Пересечение этих множеств ![]() . Число 45 является общим делителем чисел
135 и –180 и делится на все остальные общие делители этих чисел. Значит,
. Число 45 является общим делителем чисел
135 и –180 и делится на все остальные общие делители этих чисел. Значит, ![]() . Заметим, что 45 – наибольший по величине
положительный общий делитель чисел 135 и –180.
. Заметим, что 45 – наибольший по величине
положительный общий делитель чисел 135 и –180.
Упражнение. Для любых целых чисел ![]() их наибольший общий делитель является
большим по величине положительным общим делителем. Доказать.
их наибольший общий делитель является
большим по величине положительным общим делителем. Доказать.
Из определения 2 ещё не следует, что наибольший общий делитель любого конечного множества целых существует. Докажем существование, описав способ нахождения наибольшего общего делителя, предложенный древнегреческим математиком Евклидом. Алгоритм Евклида основан на следующих леммах.
Лемма 1. Если ![]() , то
, то ![]() .
.
Доказательство. Т.к. ![]() и
и ![]() , то
, то ![]() - общий делитель
- общий делитель ![]() и
и
![]() . Если
. Если ![]() - любой
общий делитель чисел
- любой
общий делитель чисел ![]() и
и ![]() , то он
– делитель
, то он
– делитель ![]() . Оба условия выполнены, значит
. Оба условия выполнены, значит ![]() .
.
Лемма 2. Если ![]() , где
, где ![]() ,
, ![]() и
и ![]() отличны от нуля, то
отличны от нуля, то ![]() .
.
Доказательство. Пусть ![]() -
общий делитель
-
общий делитель ![]() и
и ![]() , тогда
, тогда ![]() и
и ![]() . Т.к.
. Т.к. ![]() , то
, то ![]() и
и ![]() . Поэтому любой общий делитель чисел
. Поэтому любой общий делитель чисел ![]() и
и ![]() является
общим делителем чисел
является
общим делителем чисел ![]() и
и ![]() . Пусть
теперь
. Пусть
теперь ![]() - общий делитель
- общий делитель ![]() и
и
![]() , т.е.
, т.е. ![]() ,
, ![]() . Тогда и
. Тогда и ![]() делится
на
делится
на ![]() , поэтому любой общий делитель
, поэтому любой общий делитель ![]() и
и ![]() является
общим делителем
является
общим делителем ![]() и
и ![]() . Таким
образом, множество
. Таким
образом, множество ![]() общих делителей
общих делителей ![]() и
и ![]() совпадает
с множеством
совпадает
с множеством ![]() общих делителей
общих делителей ![]() и
и
![]() , т.е.
, т.е. ![]() .
.
Пусть ![]() . Тогда
. Тогда ![]() ,
, ![]() делится
на любое число из множества
делится
на любое число из множества ![]() . Т.к.
. Т.к. ![]() , то
, то ![]() ,
, ![]() делится на любое число из
делится на любое число из ![]() .
.
Равенство ![]() доказано.
доказано.
Алгоритм Евклида состоит в следующем. Сначала ![]() делят на
делят на ![]() (
(![]() ). если
). если ![]() , то по
лемме 1
, то по
лемме 1 ![]() . В противном случае
. В противном случае ![]() . Делим
. Делим ![]() на
на ![]() . Если
. Если ![]() , то
, то ![]() , но тогда и
, но тогда и ![]() . Если
. Если ![]() не делится на
не делится на ![]() , то
получится остаток
, то
получится остаток ![]() . Делим
. Делим ![]() на
на
![]() и т.д.
и т.д.
Остатки, получаемые в процессе деления, убывают и являются натуральными числами, значит, на некотором шаге получим деление без остатка.
Последний не равный нулю остаток является наибольшим общим
делителем чисел ![]() и
и ![]() .
Сформулируем это утверждение в виде теоремы.
.
Сформулируем это утверждение в виде теоремы.
Теорема 2. Если
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
………………………….
![]() ,
, ![]() ,
,
![]() ,
,
то ![]()
Доказательство. По лемме 2 из первой строки
получаем ![]() , из второй строки снова по лемме 2:
, из второй строки снова по лемме 2: ![]() , из третьей:
, из третьей: ![]() , т.д.
Значит
, т.д.
Значит ![]() . Но
. Но ![]() и по
лемме 1:
и по
лемме 1: ![]() .
.
Пример. Найдём ![]() .
.
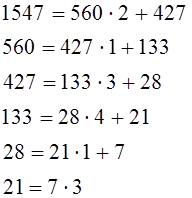
![]()
Следствие из теоремы 2. Пусть ![]() ,
, ![]() . тогда
существуют такие целые числа
. тогда
существуют такие целые числа ![]() и
и ![]() , что
, что ![]() .
Другими словами, наибольший общий делитель двух чисел можно представить в виде
линейной комбинации этих чисел с целыми коэффициентами.
.
Другими словами, наибольший общий делитель двух чисел можно представить в виде
линейной комбинации этих чисел с целыми коэффициентами.
Схема доказательства. Проходя
последовательность равенств в алгоритме Евклида снизу вверх и выражая каждый
раз ![]() через всё более ранние остатки, получим
выражение
через всё более ранние остатки, получим
выражение ![]() через
через ![]() и
и ![]()
Продолжение примера.
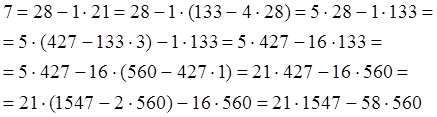
Пусть 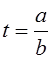 ,
, ![]() ,
, ![]() ,
, ![]() - целые. Число
- целые. Число ![]() можно
представить в виде дроби особого вида. Это представление получается из
алгоритма Евклида. Применим алгоритм Евклида к числам
можно
представить в виде дроби особого вида. Это представление получается из
алгоритма Евклида. Применим алгоритм Евклида к числам ![]() и
и
![]() . Получим:
. Получим:
![]() ,
, 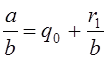 ,
,
![]() ,
, 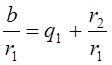 ,
,
![]() ,
, 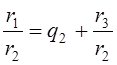 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.