Алгебраическая операция. Коммутативные и ассоциативные операции. Смежные классы по подгруппе. Теорема Лагранжа, страница 5

…………………….                   …………………                               (1)

,                   ,

,                              

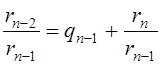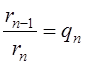
Из второго равенства получаем:

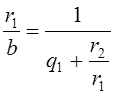                                                                                         (2)

Подставим это выражение в первое из равенств (1), получим:

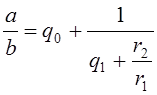                                                                                  (3)

Третье из равенств (1) даёт:

                                                  

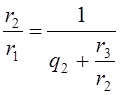
Подставим это выражение в (3), получим:

                                                  

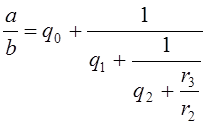
Продолжая действовать аналогично, за конечное число шагов получим:

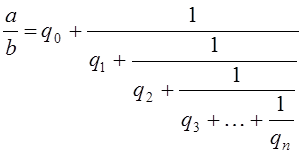                                                          (4)

Определение. Дробь вида (4) называется конечной цепной (другое название: непрерывной) дробью.

Сокращенная (и, конечно, более удобная) запись:

Числа  называются неполными частными, все они  - целые, а начиная с - натуральные.

Равенство вида (4) называется представлением рационального числа конечной цепной дробью.

Теорема. Всякое рациональное число может быть представлено в виде конечной цепной дроби.

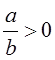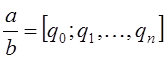Доказательство. 1-й случай: . Если , то  - натуральное число, и , если , то , .

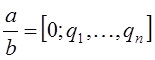2-й случай: 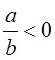. Представим дробь в виде 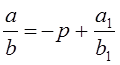, здесь  - натуральное, ,  - натуральные,  - правильная положительная дробь. Теперь 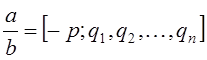, . Здесь целое ,  - натуральные.

Заметим ещё, что если 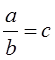 - целое, то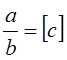

Теорема доказана.

Примеры.

1) 

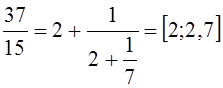
2) 

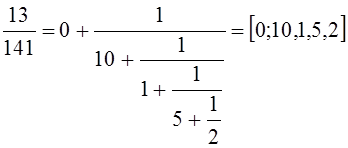
3) 

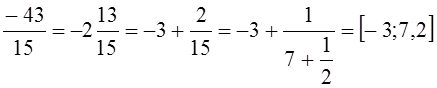
4) 

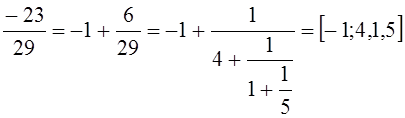
5) 

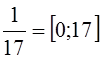
6) 

7) 

Если допустить, что последнее неполное частное может равняться 1, то для всякого рационального числа можно получить два представления в виде конечной цепной дроби.

Пример.

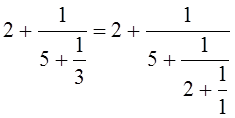
Теорема. Представление рационального числа в виде конечной цепной дроби, такой, что последнее неполное частное отлично от 1,  единственно.

Теорема. Всякая конечная цепная дробь есть рациональное число.

Доказательство. Пусть дана дробь вида (4). Если произвести арифметические действия над целыми числами 1 и , то получим рациональное число.
Обратимые элементы в кольце вычетов

1. Приведённая система вычетов.

Докажем следующую теорему:

Теорема 1. Числа одного и того же класса вычетов по модулю  имеют с один и тот же общий делитель: если , то .

Доказательство. Пусть . Тогда , - целое. Из этого равенства следует, что .

Определение 1. Наибольший общий делитель модуля  и любого числа  из данного класса вычетов по  называется наибольшим общим делителем  и этого класса вычетов.

Определение 2. Класс вычетов  по модулю  называется взаимно простым с модулем , если наибольший общий делитель  и  равен 1 (т.е. если  и любое число из  взаимно просты).

Пример. Пусть . Класс вычетов  состоит из чисел . Наибольший общий делитель любого из этих чисел и модуля 6 равен 2. Значит, . Наибольший общий делитель любого числа из класса  и модуля 6 равен 1. Значит, класс  взаимно прост с модулем 6.

Выберем из каждого класса вычетов, взаимно простого с модулем , по одному числу. Получим систему вычетов, составляющую часть полной системы вычетов. Её называют приведённой системой вычетов по модулю  .

Определение 3. Совокупность вычетов по модулю , взятых по одному из каждого взаимно простого с  класса вычетов по этому модулю, называется приведённой системой вычетов.

2. Мультипликативная группа обратимых элементов в кольце вычетов.

Описание обратимых элементов в кольце вычетов  даётся следующей теоремой:

Теорема 2. Для того, чтобы класс вычетов  по модулю  был обратимым, необходимо и достаточно, чтобы  и  были взаимно простыми.

Доказательство. Пусть класс вычетов  взаимно прост с . Выберем в  число . Так как  и  взаимно просты, то найдутся такие числа  и , что . Тогда , значит  делится на , поэтому . Отсюда следует, что , где  - класс вычетов, содержащий . Это и значит, что  - обратимый класс в .